题目内容
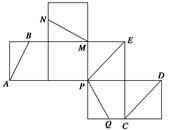
如图,两矩形ABCD,ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为 ,M、N分别为DE与DB的中点,且MN=1.
,M、N分别为DE与DB的中点,且MN=1.
(1) 求证:MN丄平面ABCD
(2) 求线段AB的长;
(3) 求二面角A—DE—B的平面角的正弦值.

 ,M、N分别为DE与DB的中点,且MN=1.
,M、N分别为DE与DB的中点,且MN=1.(1) 求证:MN丄平面ABCD
(2) 求线段AB的长;
(3) 求二面角A—DE—B的平面角的正弦值.

(Ⅰ)证明:∵平面ABCD⊥平面ABEF,且平面ABCD 平面ABEF=AB
平面ABEF=AB
EB⊥AB ∴EB⊥平面ABCD 又MN∥EB
∴MN⊥面ABCD. (3分)
(Ⅱ)由(Ⅰ)可知∠EDB为DE与平面ABCD所成的角 ∴∠EDB=30o
又在Rt△EBD中,EB=2MN=2,∠EBD=90o ∴DE=
连结AE,可知∠DEA为DE与平面ABEF所成的角 ∴∠DEA=45o(5分)
在Rt△DAE中,∠DAE=90o ∴AE=DE cos∠DEA=2
在Rt△ABE中, . (7分)
. (7分)

(Ⅲ)方法一:过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH
∵AD⊥平面ABEF BO 面ABEF
面ABEF
∴BO⊥平面ADE ∴OH为BH在平面ADE内的射影
∴BH⊥DE 即∠BHO为所求二面角的平面角 (9分)
在Rt△ABE中,BO=
在Rt△DBE中,由BH·DE=DB·OE得BH=
∴sin∠BHO=
 平面ABEF=AB
平面ABEF=ABEB⊥AB ∴EB⊥平面ABCD 又MN∥EB
∴MN⊥面ABCD. (3分)
(Ⅱ)由(Ⅰ)可知∠EDB为DE与平面ABCD所成的角 ∴∠EDB=30o
又在Rt△EBD中,EB=2MN=2,∠EBD=90o ∴DE=

连结AE,可知∠DEA为DE与平面ABEF所成的角 ∴∠DEA=45o(5分)
在Rt△DAE中,∠DAE=90o ∴AE=DE cos∠DEA=2

在Rt△ABE中,
 . (7分)
. (7分)
(Ⅲ)方法一:过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH
∵AD⊥平面ABEF BO
 面ABEF
面ABEF∴BO⊥平面ADE ∴OH为BH在平面ADE内的射影
∴BH⊥DE 即∠BHO为所求二面角的平面角 (9分)
在Rt△ABE中,BO=

在Rt△DBE中,由BH·DE=DB·OE得BH=

∴sin∠BHO=

略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,AE∥CD,DC=AC=2AE=2.
,AE∥CD,DC=AC=2AE=2. CD
CD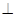 平面ABC
平面ABC
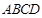 的长方体被截面
的长方体被截面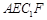 所截
所截 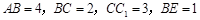 .
. ;
;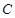 到平面
到平面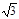
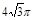
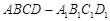 的表面上有一动点P由顶点A出发按下列规则向点
的表面上有一动点P由顶点A出发按下列规则向点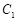 移动:①点P只能沿正方体木块的棱或表面对角线移动;②点P每一变化位置,都使P点到点
移动:①点P只能沿正方体木块的棱或表面对角线移动;②点P每一变化位置,都使P点到点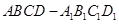 中,
中,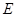 为
为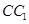 的中点.
的中点.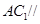 平面
平面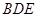 ;
; 在棱
在棱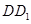 上什么位置时,平面
上什么位置时,平面 平面
平面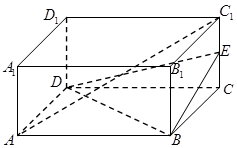
 、
、 为圆柱
为圆柱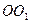 的母线,
的母线,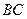 是底面圆
是底面圆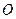 的直径,
的直径,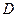 、
、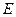 分别是
分别是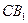 的中点,
的中点,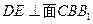 .
.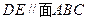 ;
;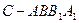 与圆柱
与圆柱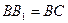 ,求
,求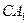 与面
与面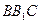 所成角的正弦值.
所成角的正弦值.
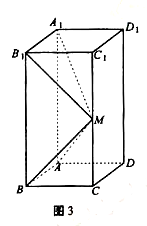
 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点