题目内容
定义在(-1,0)内的函数f(x)=log2-a(x+1)满足f(x)>0恒成立,则实数a的取值范围是 .
考点:对数函数的图像与性质
专题:
分析:根据单调性得出0<2-a<1,0<2-a<1,得出即可.
解答:
解:∵定义在(-1,0),
∴0<x+1<1,
∵f(x)=log2-a(x+1)满足f(x)>0恒成立,
求解得出:0<2-a<1,
0<2-a<1,
即1<a<2,
故答案为:1<a<2.
∴0<x+1<1,
∵f(x)=log2-a(x+1)满足f(x)>0恒成立,
求解得出:0<2-a<1,
0<2-a<1,
即1<a<2,
故答案为:1<a<2.
点评:本题考查了对数函数的单调性,解不等式,属于中档题,关键得出不等即可.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
函数f(x)=2x3的图象( )
| A、关于y轴对称 |
| B、关于x轴对称 |
| C、关于直线y=x对称 |
| D、关于原点对称 |
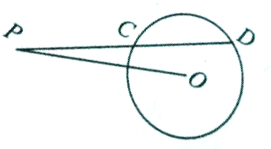 已知圆O的半径为1,过圆外一点P作圆O的割线与圆O交于C,D两点,若PC•PD=8,则线段PO的长度为
已知圆O的半径为1,过圆外一点P作圆O的割线与圆O交于C,D两点,若PC•PD=8,则线段PO的长度为