Question

解不等式|x+7|-|x-2|≤3.

Answer 1

思路分析：解含有绝对值的不等式，总的思路是同解变形为不含绝对值的不等式，但要根据求解不等式的结构，选用恰当的方法.此题中有两个绝对值符号，故可用绝对值的几何意义来求解，或用分区间讨论法求解，还可构造函数利用函数图象求解.

                                 图1

解：［方法一］ |x+7|-|x-2|可以看成数轴上的动点(坐标为x)到-7对应的点的距离与到2对应的点的距离的差，先找到这个差等于3的点，即x=-1（如图1所示）.

从图易知不等式|x+7|-|x-2|≤3的解为x≤-1，即x∈(-∞,-1］.

［方法二］ 令x+7=0，x-2=0得x=-7，x=2.

①当x＜-7时，不等式变为-x-7+x-2≤3，

∴-9≤3成立,∴x＜-7.

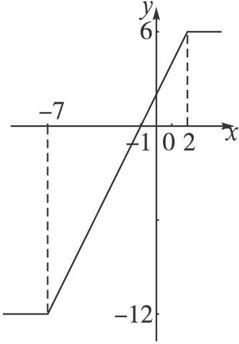
                       图2

②当-7≤x≤2时，不等式变为x+7+x-2≤3，

即2x≤-2，∴x≤-1，

∴-7≤x≤-1.

③当x＞2时，不等式变为x+7-x+2≤3，

即9≤3不成立，∴x∈.

∴原不等式的解集为(-∞,-1］.

［方法三］ 将原不等式转化为|x+7|-|x-2|-3≤0，

构造函数y=|x+7|-|x-2|-3，即

y=.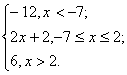

    作出函数的图象（如图2），从图可知，当x≤-1时，有y≤0，

即|x+7|-|x-2|-3≤0，

所以，原不等式的解集为(-∞,-1］.

    巧妙变式

    针对此题，我们可以进行各种不同的题目变式.如：可以将两个绝对值里面的运算符号改变、可以将两个绝对值之间的运算符号改变、可以将“≤”改变为“≥”，还可以将不等号右边的数改成字母等等.变式后题目的求解还是用上述的几种解法.