题目内容
在极坐标系中,过曲线L: (
( >0)外的一点A(2
>0)外的一点A(2 ,
, )(其中tanθ=2,θ为锐角)作平行于θ=
)(其中tanθ=2,θ为锐角)作平行于θ= (
( )的直线
)的直线 与曲线L分别交于B、C。
与曲线L分别交于B、C。
(1)写出曲线L和直线 的普通方程(以极点为原点,极轴为x轴的正半轴建系);(2)若︱AB︱、︱BC︱、︱AC︱成等比数列,求
的普通方程(以极点为原点,极轴为x轴的正半轴建系);(2)若︱AB︱、︱BC︱、︱AC︱成等比数列,求 的值。
的值。
 (
( >0)外的一点A(2
>0)外的一点A(2 ,
, )(其中tanθ=2,θ为锐角)作平行于θ=
)(其中tanθ=2,θ为锐角)作平行于θ= (
( )的直线
)的直线 与曲线L分别交于B、C。
与曲线L分别交于B、C。(1)写出曲线L和直线
 的普通方程(以极点为原点,极轴为x轴的正半轴建系);(2)若︱AB︱、︱BC︱、︱AC︱成等比数列,求
的普通方程(以极点为原点,极轴为x轴的正半轴建系);(2)若︱AB︱、︱BC︱、︱AC︱成等比数列,求 的值。
的值。(1)L:y2=2ax,A(-2,-4)  :y=x-2(2)a=1
:y=x-2(2)a=1
 :y=x-2(2)a=1
:y=x-2(2)a=1本试题主要是考查了极坐标方程与直角坐标方程的转化,以及等比数列的概念的运用。
(1)因为过曲线L: ,两边同时乘以
,两边同时乘以 化简为直角坐标方程。
化简为直角坐标方程。
(2)将 与抛物线联立得到二次方程,结合数列的关系式︱BC︱2=︱AB︱︱AC︱,和t的几何意义得到参数a的值。
与抛物线联立得到二次方程,结合数列的关系式︱BC︱2=︱AB︱︱AC︱,和t的几何意义得到参数a的值。
(1)L:y2=2ax,A(-2,-4) :y=x-2
:y=x-2
 与抛物线联立得t2-2
与抛物线联立得t2-2 (4+a)t+8(4+a)=0
(4+a)t+8(4+a)=0
由已知:︱BC︱2=︱AB︱︱AC︱,由t的几何意义︱t1-t2︱2=︱t1t2︱得a=1
(1)因为过曲线L:
 ,两边同时乘以
,两边同时乘以 化简为直角坐标方程。
化简为直角坐标方程。(2)将
 与抛物线联立得到二次方程,结合数列的关系式︱BC︱2=︱AB︱︱AC︱,和t的几何意义得到参数a的值。
与抛物线联立得到二次方程,结合数列的关系式︱BC︱2=︱AB︱︱AC︱,和t的几何意义得到参数a的值。(1)L:y2=2ax,A(-2,-4)
 :y=x-2
:y=x-2 与抛物线联立得t2-2
与抛物线联立得t2-2 (4+a)t+8(4+a)=0
(4+a)t+8(4+a)=0由已知:︱BC︱2=︱AB︱︱AC︱,由t的几何意义︱t1-t2︱2=︱t1t2︱得a=1

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 ,则它的极坐标是( )
,则它的极坐标是( )



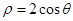 的圆心到直线
的圆心到直线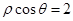 的距离是__________.
的距离是__________. 关于极点的对称点可以为( )
关于极点的对称点可以为( )



 和直线
和直线 ,
, 的直角坐标方程;
的直角坐标方程; 时,求直线
时,求直线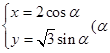 为参数).
为参数). 与圆
与圆 相交的弦长为
相交的弦长为  被圆
被圆 所截得的弦长为________
所截得的弦长为________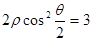 化为直角坐标方程是 .
化为直角坐标方程是 .