题目内容
设函数f(x)=x2-(a-2)x-alnx.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)已知方程f(x)=c(c为常数)有两个不相等的实数根x1,x2.
(i)若c=0,求满足条件的最小正整数a的值;
(ii)求证:f′(
)>0.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)已知方程f(x)=c(c为常数)有两个不相等的实数根x1,x2.
(i)若c=0,求满足条件的最小正整数a的值;
(ii)求证:f′(
| x1+x2 |
| 2 |
考点:利用导数研究函数的单调性,导数的运算,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)对a分类讨论,利用导数与函数单调性的关系即可得出;
(2)由(1)可得,若函数f(x)有两个不相等的实数根x1,x2,则a>0,且f(x)的最小值f(
)<0,
即-a2+4a-4aln
<0.得出h(a)=a+4ln
-4>0.利用单调性判断其零点所处的最小区间即可得出;
(3))由x1,x2是方程f(x)=c得两个不等实数根,则
-(a-2)x1-alnx1=c,
-(a-2)x2-alnx2=c两式相减,得出a=
,换元,再利用导数即可证明.
(2)由(1)可得,若函数f(x)有两个不相等的实数根x1,x2,则a>0,且f(x)的最小值f(
| a |
| 2 |
即-a2+4a-4aln
| a |
| 2 |
| a |
| 2 |
(3))由x1,x2是方程f(x)=c得两个不等实数根,则
| x | 2 1 |
| x | 2 2 |
| ||||
| x1+lnx1-x2-lnx2 |
解答:
解:(1)f′(x)=
(x>0)
当a≤0时,f'(x)>0,函数f(x)在(0,+∞)上单调递增,
∴函数f(x)的单调增区间为(0,+∞)
当a>0时,由f'(x)>0得x>
;由f'(x)<0得0<x<
,
∴函数f(x)的单调增区间为(
,+∞),单调减区间为(0,
)
(2)由(1)可得,若函数f(x)有两个不相等的实数根x1,x2.
则a>0,且f(x)的最小值f(
)<0,
即-a2+4a-4aln
<0.
∵a>0,∴a+4ln
-4>0.
令h(a)=a+4ln
-4,可知h(a)在(0,+∞)上为增函数,且h(2)=-2,h(3)=4ln
-1=ln
-1>lne-1=0,
所以存在零点h(a0)=0,a0∈(2,3),
当a>a0时,h(a)>0;当0<a<a0时,h(a)<0.
所以满足条件的最小正整数a=3.
又当a=3时,f(3)=3(2-ln3)>0,f(1)=0,∴a=3时,f(x)由两个零点.
综上所述,满足条件的最小正整数a的值为3.
(3)∵x1,x2是方程f(x)=c的两个不等实根,不妨设0<x1<x2
则
-(a-2)x1-alnx1=c,
-(a-2)x2-alnx2=c
两式相减得
-(a-2)x1-alnx1-(
-(a-2)x2-alnx2)=0,
即a=
,
又∵f′(
)=0,当x>
时f'(x)>0;
当 0<x<
时f'(x)<0
故只要证明
>
即可,
即证x1+x2>
即证明:ln
<
,
设t=
(0<t<1),
令g(t)=lnt-
,
则g′(t)=
≥0,
则g(t)=lnt-
在(0,+∞)为增函数,
又∵g(1)=0,
∴t∈(0,1)时,g(t)<0总成立,得证.
| (2x-a)(x+1) |
| x |
当a≤0时,f'(x)>0,函数f(x)在(0,+∞)上单调递增,
∴函数f(x)的单调增区间为(0,+∞)
当a>0时,由f'(x)>0得x>
| a |
| 2 |
| a |
| 2 |
∴函数f(x)的单调增区间为(
| a |
| 2 |
| a |
| 2 |
(2)由(1)可得,若函数f(x)有两个不相等的实数根x1,x2.
则a>0,且f(x)的最小值f(
| a |
| 2 |
即-a2+4a-4aln
| a |
| 2 |
∵a>0,∴a+4ln
| a |
| 2 |
令h(a)=a+4ln
| a |
| 2 |
| 3 |
| 2 |
| 81 |
| 16 |
所以存在零点h(a0)=0,a0∈(2,3),
当a>a0时,h(a)>0;当0<a<a0时,h(a)<0.
所以满足条件的最小正整数a=3.
又当a=3时,f(3)=3(2-ln3)>0,f(1)=0,∴a=3时,f(x)由两个零点.
综上所述,满足条件的最小正整数a的值为3.
(3)∵x1,x2是方程f(x)=c的两个不等实根,不妨设0<x1<x2
则
| x | 2 1 |
| x | 2 2 |
两式相减得
| x | 2 1 |
| x | 2 2 |
即a=
| ||||
| x1+lnx1-x2-lnx2 |
又∵f′(
| a |
| 2 |
| a |
| 2 |
当 0<x<
| a |
| 2 |
故只要证明
| x1+x2 |
| 2 |
| a |
| 2 |
即证x1+x2>
| ||||
| x1+lnx1-x2-lnx2 |
即证明:ln
| x1 |
| x2 |
| 2x1-2x2 |
| x1+x2 |
设t=
| x1 |
| x2 |
令g(t)=lnt-
| 2t-2 |
| t+1 |
则g′(t)=
| (t-1)2 |
| t(t+1)2 |
则g(t)=lnt-
| 2t-2 |
| t+1 |
又∵g(1)=0,
∴t∈(0,1)时,g(t)<0总成立,得证.
点评:本题综合考查了利用导数研究函数的单调性、极值与最值等基础知识,及其分类讨论思想方法、等价转化方法、换元法等基本技能与方法.

练习册系列答案
相关题目
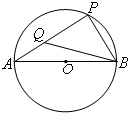 如图,AB是半径为3的圆O的直径,P是圆O上异于A,B的一点Q是线段AP上靠近A的三等分点,且
如图,AB是半径为3的圆O的直径,P是圆O上异于A,B的一点Q是线段AP上靠近A的三等分点,且