题目内容
9.如图,在边长为1的正方形OABC中任取一点,则该点落在阴影部分中的概率为$\frac{1}{3}$.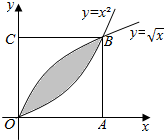
分析 根据题意,易得正方形OABC的面积,观察图形,由定积分公式计算阴影部分的面积,进而由几何概型公式计算可得答案.
解答 解:根据题意,正方形OABC的面积为1×1=1,
由函数y=x与y=$\sqrt{x}$围成阴影部分的面积为∫01($\sqrt{x}$-x)dx=($\frac{2}{3}{x}^{\frac{3}{2}}$-$\frac{{x}^{2}}{2}$)|01=$\frac{1}{6}$,
由于y=x2与y=$\sqrt{x}$互为反函数,所以阴影部分的面积为$\frac{1}{3}$,
则正方形OABC中任取一点P,点P取自阴影部分的概率为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查几何概型的计算,涉及定积分在求面积中的应用,关键是正确计算出阴影部分的面积.

练习册系列答案
相关题目
4.已知f(x)=$\frac{1}{2}$x2+$\frac{b}{x}$+c(b,c为常数)和g(x)=$\frac{1}{4}$x+$\frac{1}{x}$是定义在M={x|1≤x≤4}上的函数,对任意的x∈M,存在x0∈M使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0),则f(x)在集合M上的最大值为( )
| A. | $\frac{7}{2}$ | B. | 5 | C. | 6 | D. | 8 |
1.已知函数$f(x)=\left\{{\begin{array}{l}{{x^2}+1}\\{-2x}\end{array}}\right.$$\begin{array}{l}(x≤0)\\(x>0)\end{array}$,若f(x)=5,则x的值是( )
| A. | -2 | B. | 2或$-\frac{5}{2}$ | C. | 2或-2 | D. | 2或-2或$-\frac{5}{2}$ |