题目内容
 如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.(1)求证:PA∥平面BDE;
(2)求证:平面PAC⊥平面BDE;
(3)若OP=10,AB=4,求BE与底面ABCD所成角的正切值.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离,空间角
分析:(1)先根据中位线定理得到OE∥AP,进而再由线面平行的判定定理可得到PA∥平面BDE.
(2)先根据线面垂直的性质定理得到PO⊥BD,结合AC⊥BD根据线面垂直的判定定理得到BD⊥平面PAC,从而根据面面垂直的判定定理得到平面PAC⊥平面BDE,得证;
(3)取OC的中点F,连接EF和BF,可得∠EBF为BE与底面ABCD所成角,即可求出BE与底面ABCD所成角的正切值.
(2)先根据线面垂直的性质定理得到PO⊥BD,结合AC⊥BD根据线面垂直的判定定理得到BD⊥平面PAC,从而根据面面垂直的判定定理得到平面PAC⊥平面BDE,得证;
(3)取OC的中点F,连接EF和BF,可得∠EBF为BE与底面ABCD所成角,即可求出BE与底面ABCD所成角的正切值.
解答:
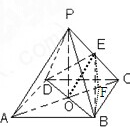 证明:(1)连接OE,
证明:(1)连接OE,
在△CAP中,CO=OA,CE=EP
∴PA∥EO,
又∵PA?平面BDE,EO?平面BDE,
∴PA∥平面BDE;
(2)∵PO⊥底面ABCD,
PO⊥BD,
又∵AC⊥BD,且AC∩PO=O,
∴BD⊥平面PAC.
∵BD?平面BDE,
∴平面PAC⊥平面BDE;
(3)取OC的中点F,连接EF和BF,则OP∥EF,EF=5
又∵OP⊥底面ABCD,∴EF⊥底面ABCD,
∴∠EBF为BE与底面ABCD所成角.
∵OF=
OB=
,BF=
=
,
∴tan∠EBF=
=
.
 证明:(1)连接OE,
证明:(1)连接OE,在△CAP中,CO=OA,CE=EP
∴PA∥EO,
又∵PA?平面BDE,EO?平面BDE,
∴PA∥平面BDE;
(2)∵PO⊥底面ABCD,
PO⊥BD,
又∵AC⊥BD,且AC∩PO=O,
∴BD⊥平面PAC.
∵BD?平面BDE,
∴平面PAC⊥平面BDE;
(3)取OC的中点F,连接EF和BF,则OP∥EF,EF=5
又∵OP⊥底面ABCD,∴EF⊥底面ABCD,
∴∠EBF为BE与底面ABCD所成角.
∵OF=
| 1 |
| 2 |
| 2 |
| OB2+OF2 |
| 10 |
∴tan∠EBF=
| EF |
| BF |
| ||
| 2 |
点评:本题考查线面平行的判定与面面垂直的判定.证明线面平行常有两种思路:一是线线平行⇒线面平行;二是面面平行⇒线面平行.证明面面垂直的常用方法是:线面垂直⇒面面垂直.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知定义在R上的函数f(x)满足:对任意x,都有f(1+x)=f(1-x),且f(x)在(-∞,1]上是单调递增,若x1<x2,且x1+x2=3,则f(x1)与f(x2)的大小关系是( )
| A、f(x1)<f(x2) |
| B、f(x1)=f(x2) |
| C、f(x1)>f(x2) |
| D、不能确定 |
函数y=|sinx|的最小正周期为( )
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |

