题目内容
(2012•泰安一模)已知函数f(x)=x2-(2a+1)x+alnx.
(I)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(II)求函数f(x)的单调区间.
(I)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(II)求函数f(x)的单调区间.
分析:(I)当a=2时,f(x)=x2-5x+2lnx,由f′(x)=2x-5+
,知f′(1)=2-5+2=-1,由此能够求出曲线y=f(x)在点(1,f(1))处的切线方程.
(II)f′(x)=2x-(2a+1)+
=
,令f′(x)=0,得x1=
,x2 =a.由此进行分类讨论,能够求出结果.
| 2 |
| x |
(II)f′(x)=2x-(2a+1)+
| a |
| x |
| 2x2-(2a+1)x+a |
| x |
| 1 |
| 2 |
解答:解:(I)当a=2时,f(x)=x2-(2a+1)x+alnx=x2-5x+2lnx,
∴f′(x)=2x-5+
,
∴f′(1)=2-5+2=-1,
∵f(1)=1-5=-4,
∴曲线y=f(x)在点(1,f(1))处的切线方程为:x+y+3=0.
(II)f′(x)=2x-(2a+1)+
=
,
令f′(x)=0,得x1=
,x2 =a.
①当a>
时,由f′(x)>0,得x>a,或x<
,
f(x)在(0,
),(a,+∞)是单调递增.
由f′(x)<0,得
<x<a,
∴f(x)在(
,a)上单调递减.
②当a=
时,f′(x)≥0恒成立,
∴f(x)在(0,+∞)上单调递增.
③当0<a<
时,由f′(x)>0,得0<x<a,或x>
,
∴f(x)在(0,a),(
,+∞)上单调增加,
由f′(x)<0,得a<x<
,
∴f(x)在(a,
)上单调递减.
④当a≤0时,由f′(x)>0,得x>
,
∴f(x)在(
,+∞)上单调递增.
由f′(x)<0,得0<x<
,
∴f(x)在(0,
)上单调递减.
∴f′(x)=2x-5+
| 2 |
| x |
∴f′(1)=2-5+2=-1,
∵f(1)=1-5=-4,
∴曲线y=f(x)在点(1,f(1))处的切线方程为:x+y+3=0.
(II)f′(x)=2x-(2a+1)+
| a |
| x |
| 2x2-(2a+1)x+a |
| x |
令f′(x)=0,得x1=
| 1 |
| 2 |
①当a>
| 1 |
| 2 |
| 1 |
| 2 |
f(x)在(0,
| 1 |
| 2 |
由f′(x)<0,得
| 1 |
| 2 |
∴f(x)在(
| 1 |
| 2 |
②当a=
| 1 |
| 2 |
∴f(x)在(0,+∞)上单调递增.
③当0<a<
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)在(0,a),(
| 1 |
| 2 |
由f′(x)<0,得a<x<
| 1 |
| 2 |
∴f(x)在(a,
| 1 |
| 2 |
④当a≤0时,由f′(x)>0,得x>
| 1 |
| 2 |
∴f(x)在(
| 1 |
| 2 |
由f′(x)<0,得0<x<
| 1 |
| 2 |
∴f(x)在(0,
| 1 |
| 2 |
点评:本题考查利用导数求曲线上某点处的切线方程的应用,解题时要认真审题,仔细解答,注意函数的单调性的灵活运用.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
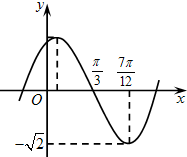 (2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则
(2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则