$\frac{sin40°\sqrt{1+cos80°}}{\sqrt{1-2sin10°cos10°}+sin10°}$的值为( )A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\sqrt{2}$D．$\sqrt{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

12．$\frac{sin40°\sqrt{1+cos80°}}{\sqrt{1-2sin10°cos10°}+sin10°}$的值为（　　）

A．

$\frac{1}{2}$

B．

$\frac{\sqrt{2}}{2}$

C．

$\sqrt{2}$

D．

$\sqrt{3}$

分析利用三角恒等变换化简所给的式子，可得结果．

解答解：$\frac{sin40°\sqrt{1+cos80°}}{\sqrt{1-2sin10°cos10°}+sin10°}$=$\frac{sin40°•\sqrt{2}cos40°}{cos10°-sin10°+sin10°}$=$\frac{\frac{\sqrt{2}}{2}sin80°}{cos10°}$=$\frac{\sqrt{2}}{2}$，
故选：B．

点评本题主要考查三角函数的恒等变换及化简求值，属于基础题．

练习册系列答案

3．若不等式$\frac{1}{2}{x^2}-{y^2}$≤2cx（y-x）对任意满足x＞y＞0的实数x，y恒成立，则实数c的最大值为$\frac{\sqrt{2}}{2}-1$．

20．已知点A（-1，-2），B（3，8），若$\overrightarrow{AB}=2\overrightarrow{AC}$，则点C的坐标为（1，3）．

7．

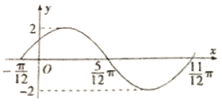函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示．
（1）求函数y=f（x）的解析式；
（2）将函数y=f（x）的图象向右平移$\frac{π}{4}$个单位，得到函数y=g（x）的图象，若$f（{\frac{α}{2}}）=\frac{1}{2}，α∈（{\frac{π}{3}，\frac{5π}{6}}）$，求g（α）的值．

17．若$\frac{sinα-cosα}{sinα+cosα}$=2，则tan（α-$\frac{π}{4}$）=2．

1．已知数列{a_n}的通项公式为a_n=$\frac{1}{3n-2}$，n∈N^*．
（1）求数列{$\frac{{a}_{n}+2}{{a}_{n}}$}的前n项和S_n；
（2）设b_n=a_na_n+1，求{b_n}的前n项和T_n．

18．在△ABC中，若b²=ac，则cos（A-C）+cosB+cos2B-2的值是-1．

19．（1）已知0＜a＜1，0＜b＜1，0＜c＜1，用分析法证明：$\frac{a+b+c+abc}{1+ab+bc+ca}≤1$
（2）已知a+b+c=0，ab+bc+ca＞0且abc＞0，用反证法证明：a，b，c都大于零．

试题分类