题目内容

已知
sin(α+2β)
sinα
=3，且β≠
1
2
kπ，α+β≠nπ+
π
2
（n，k∈Z），则
tan(α+β)
tanβ
的值为（　　）
A．2B．1C．
1
2
D．-2
∵
sin(α+2β)
sinα
=
sin[(α+β)+β]
sin[(α+β)-β]
=
sin(α+β)cosβ+cos(α+β)sinβ
sin(α+β)cosβ-cos(α+β)sinβ
=3，
∴3sin（α+β）cosβ-3cos（α+β）sinβ=sin（α+β）cosβ+cos（α+β）sinβ，
∴2sin（α+β）cosβ=4cos（α+β）sinβ，
又β≠
1
2
kπ，α+β≠nπ+
π
2
，（n，k∈Z），
∴
tan(α+β)
tanβ
=2．
故选：A．
练习册系列答案
相关题目
已知α，β∈R，写出用cosα，cosβ，sinα，sinβ表示cos（α-β）的关系等式，并证明这个关系等式．
已知sin（α+
π
3
）+sinα=-
4
3
5
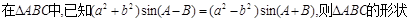，则cos(α+
2π
3
)=（　　）
A．-
4
5
B．
4
5
C．-
3
5
D．
3
5
已知
π
2
＜α＜π，sinα=
4
5

（1）求tanα的值；
（2）求cos2α+sin（π-α）的值．
sin68°sin67°-sin23°cos68°的值为（　　）
A．-
2
2
B．
2
2
C．
3
2
D．1
已知：cos（α+
π
2
）=
4
5
，且α∈(π，
3π
2
)，sin（3π-β）=-
12
13
，且β∈(
3
2
π，2π)，则sin（α+β）=______．
 （　　）
A．等腰三角形B．直角三角形
C．等腰直角三角形D．等腰三角形或直角三角形
已知，则的取值范围是（    ）．
A     B     C     D 
已知                .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网