Question

【题目】设，则的最小值为______.

Answer 1

【答案】

【解析】

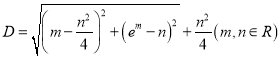设（其中，则），其几何意义为两点，的距离的平方，令，，

则，而是抛物线上的点到准线的距离，从而可以看作抛物线上的点到焦点距离和到上的点的距离的和，即的最小值是点到上的点的距离的最小值.

设（其中，则），其几何意义为两点，的距离的平方，令，，

由的导数为，，

点在曲线上，又，

令，，

则，而是抛物线上的点到准线的距离，即抛物线上的点到焦点的距离，

从而可以看作抛物线上的点到焦点距离和到上的点的距离的和，即，如图所示：

由两点之间线段最短，得的最小值是点到上的点的距离的最小值，由点到直线上垂线段最短，则就最小，即最小，

设，则，即，解得，即

点到的距离就是点到上的点的距离的最小值，

故的最小值为，即的最小值为.

故答案为：.