题目内容
已知实数x,y满足
,则
的取值范围是 .
|
| |12x-5y+39| |
| 13 |
考点:点到直线的距离公式
专题:计算题,空间位置关系与距离
分析:
的几何意义是满足
点(x,y)到直线12x-5y+13=0的距离,即可的成交量.
| |12x-5y+39| |
| 13 |
|
解答:
解:
的几何意义是满足
点(x,y)到直线12x-5y+13=0的距离,
∵圆心(0,0)到直线12x-5y+13=0的距离为1,圆的半径为2,
∴
的取值范围是[0,3],
故答案为:[0,3]
| |12x-5y+39| |
| 13 |
|
∵圆心(0,0)到直线12x-5y+13=0的距离为1,圆的半径为2,
∴
| |12x-5y+39| |
| 13 |
故答案为:[0,3]
点评:本题考查点到直线的距离公式,利用
的几何意义是满足
点(x,y)到直线12x-5y+13=0的距离是关键.
| |12x-5y+39| |
| 13 |
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=10|x+1|-1的单调减区间为( )
| A、(-∞,-1) |
| B、(-∞,1) |
| C、(-1,+∞) |
| D、(1,+∞) |
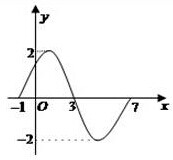 如图为函数y1=Asin(ωx+φ)(|φ|<
如图为函数y1=Asin(ωx+φ)(|φ|<