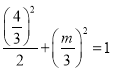题目内容
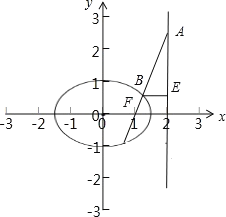
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(1)求证: ![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(Ⅰ)在平行四边形![]() 中,由条件可得
中,由条件可得![]() ,进而可得
,进而可得![]() 。由侧面
。由侧面![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() ,故得
,故得![]() ,所以可证得
,所以可证得![]() 平面
平面![]() .(Ⅱ)先证明平面
.(Ⅱ)先证明平面![]() 平面
平面![]() ,由面面平行的性质可得
,由面面平行的性质可得![]() 平面
平面![]() .(Ⅲ)建立空间直角坐标系,通过求出平面的法向量,根据线面角的向量公式可得
.(Ⅲ)建立空间直角坐标系,通过求出平面的法向量,根据线面角的向量公式可得![]() 。
。
试题解析:
(Ⅰ)证明:在平行四边形![]() 中,
中,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵侧面![]() 底面
底面![]() ,且
,且![]() ,
,
∴![]() 底面
底面![]() ,
,
又![]() 底面
底面![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)证明:∵![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
同理![]() 平面
平面![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅲ)解:由![]() 底面
底面![]() ,
, ![]() ,可得
,可得![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直,
建立如图空间直角坐标系![]() ,
,

则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
, ![]() ,
,
易得平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则:
,则:
由![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
∵直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,
所成的角相等,
∴![]() ,即
,即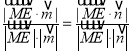 ,
,
∴![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
故![]() .
.
点睛:用向量法确定空间中点的位置的方法
根据题意建立适当的空间直角坐标系,由条件确定有关点的坐标,运用共线向量用参数(参数的范围要事先确定)确定出未知点的坐标,根据向量的运算得到平面的法向量或直线的方向向量,根据所给的线面角(或二面角)的大小进行运算,进而求得参数的值,通过与事先确定的参数的范围进行比较,来判断参数的值是否符合题意,进而得出点是否存在的结论。
【题型】解答题
【结束】
21
【题目】如图,椭圆![]() 上的点到左焦点的距离最大值是
上的点到左焦点的距离最大值是![]() ,已知点
,已知点![]() 在椭圆上,其中
在椭圆上,其中![]() 为椭圆的离心率.
为椭圆的离心率.

(1)求椭圆的方程;
(2)过原点且斜率为![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,其中
两点,其中![]() 在第一象限,它在
在第一象限,它在![]() 轴上的射影为点
轴上的射影为点![]() ,直线
,直线![]() 交椭圆于另一点
交椭圆于另一点![]() .证明:对任意的
.证明:对任意的![]() ,点
,点![]() 恒在以线段
恒在以线段![]() 为直径的圆内.
为直径的圆内.
【答案】(1)![]() .(2)证明见解析.
.(2)证明见解析.
【解析】试题分析:(1)根据椭圆上的点到左焦点为F的最大距离是![]() ,M(1,e)在椭圆上,建立方程组,即可求椭圆的方程;
,M(1,e)在椭圆上,建立方程组,即可求椭圆的方程;
(2)设出直线QN的方程,代入椭圆方程,利用韦达定理,结合向量的数量积,即可得到结论.
试题解析:
(1)由题可知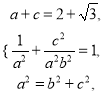 解得
解得![]() ∴椭圆的方程是
∴椭圆的方程是![]() .
.
(2)令![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,∴
,∴![]() ,
,
直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 整理得
整理得![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
, 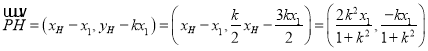 ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴对任意![]() ,点
,点![]() 恒在以线段
恒在以线段![]() 为直径的圆内.
为直径的圆内.

【题目】辽宁号航母纪念章从2012年10月5日起开始上市,通过市场调查,得到该纪念章每![]() 枚的市场价
枚的市场价![]() (单位:元)与上市时间
(单位:元)与上市时间![]() (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 |
|
|
|
市场价 |
|
|
|
(1)根据上表数据,从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系:①
的变化关系:①![]() ;②
;②![]() ;③
;③![]() ;
;
(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格;
(3)设你选取的函数为![]() ,若对任意实数
,若对任意实数![]() ,关于
,关于![]() 的方程
的方程![]() 恒有个想异实数根,求
恒有个想异实数根,求![]() 的取值范围.
的取值范围.