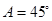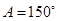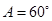题目内容
已知函数f(x)=sin(ωx+
)+sin(ωx-
)-2cos2
,x∈R(其中ω>0),若对任意的a∈R,函数y=f(x),x∈(a,a+π]的图象与直线y=-1有且仅有两个不同的交点.
(1)试确定ω的值(不必证明),并求函数f(x)在(0,
)的值域;
(2)求函数f(x)在(0,4)上的单调增区间.
| π |
| 6 |
| π |
| 6 |
| ωx |
| 2 |
(1)试确定ω的值(不必证明),并求函数f(x)在(0,
| 4π |
| 7 |
(2)求函数f(x)在(0,4)上的单调增区间.
(1)由f(x)=sin(ωx+
)+sin(ωx-
)-2cos2
,
得f(x)=sinωxcos
+cosωxsin
+sinωxcos
-cosωxsin
-(1+cosωx)
=2sinωxcos
-1-cosωx
=
sinωx-cosωx-1.
整理得:f(x)=2sin(ωx-
)-1.
∵对任意的a∈R,函数y=f(x),x∈(a,a+π]的图象与直线y=-1有且仅有两个不同的交点
∴T=π,则ω=
=
=2.
∴f(x)=2sin(2x-
)-1.
当x∈(0,
)时,2x-
∈(-
,
),
∴f(x)在(0,
)的值域为(-2,1];
(2)由-
+2kπ≤2x-
≤
+2kπ,k∈Z,
得:-
+kπ≤x≤
+kπ,k∈Z.
当k=0时,-
≤x≤
;
当k=1时,
≤x≤
.
∴函数f(x)在(0,4)上的单调增区间为(0,
),(
,4).
| π |
| 6 |
| π |
| 6 |
| ωx |
| 2 |
得f(x)=sinωxcos
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=2sinωxcos
| π |
| 6 |
=
| 3 |
整理得:f(x)=2sin(ωx-
| π |
| 6 |
∵对任意的a∈R,函数y=f(x),x∈(a,a+π]的图象与直线y=-1有且仅有两个不同的交点
∴T=π,则ω=
| 2π |
| T |
| 2π |
| π |
∴f(x)=2sin(2x-
| π |
| 6 |
当x∈(0,
| 4π |
| 7 |
| π |
| 4 |
| π |
| 6 |
| 41π |
| 42 |
∴f(x)在(0,
| 4π |
| 7 |
(2)由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
得:-
| π |
| 6 |
| π |
| 3 |
当k=0时,-
| π |
| 6 |
| π |
| 3 |
当k=1时,
| 5π |
| 6 |
| 4π |
| 3 |
∴函数f(x)在(0,4)上的单调增区间为(0,
| π |
| 3 |
| 5π |
| 6 |

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
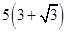 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距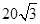 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?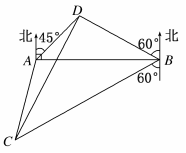
 <
< <
< <
<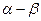 范围为(-π,π);
范围为(-π,π);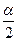 在一、三象限;
在一、三象限;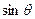 =
=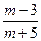 ,
,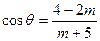 ,则m∈(3,9);
,则m∈(3,9);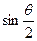 =
=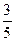 ,
,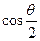 =
=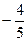 ,则
,则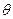 在一象限。
在一象限。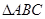 中,角
中,角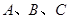 所对的边分别为
所对的边分别为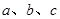 ,那么下列给出的各组条件能确定三角形有两解的是( )
,那么下列给出的各组条件能确定三角形有两解的是( )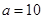 ,
,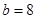 ,
,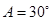
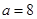 ,
,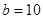 ,
,