题目内容
已知函数f(x)＝x2的图象在点A(x1，f(x1))与点B(x2，f(x2))处的切线互相垂直并交于点P，则点P的坐标可能是( )
A.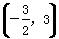
B．(0，－4)
C．(2,3) D.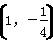
D
[解析] 由题意知，A(x1，x
)，B(x2，x
)，f′(x)＝2x，则A，B两点上的切线斜率分别为k1＝2x1，k2＝2x2，又切线互相垂直，所以k1k2＝－1，即x1x2＝－
.两条切线方程分别为l1：y＝2x1x－x，l2：y＝2x2x－x，联立得(x1－x2)[2x－(x1＋x2)]＝0，∵x1≠x2，∴x＝
，代入l1，解得y＝x1x2＝－，故选D.
练习册系列答案
一本好题口算题卡系列答案
相关题目
求(1)函数定义域;(2)函数奇偶性;(3)解不等式
－
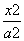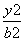＝1(a>0，b>0)的左、右焦点，若双曲线右支上存在一点P，使
＝0(O为坐标原点)，且
|，则该双曲线的离心率为________．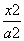
－
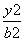＝1(a>0，b>0)的离心率为
，圆C是以坐标原点O为圆心，实轴为直径的圆．过双曲线第一象限内的任一点P(x0，y0)作圆C的两条切线，其切点分别为A，B.若直线AB与x轴、y轴分别相交于M，N两点，则
－
的值为________．
－
x2＋x＋1在区间
上有极值点，则实数a的取值范围是( )
与
平行，则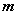
的值为（ ）
中，公比
，且
，
。
和
的值；
。