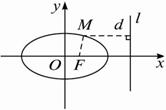
题目内容
点M(x,y)与定点F(c,0)的距离和它到定直线l:x=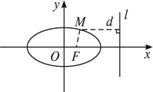
解:设d是点M到直线l的距离,
根据题意,所求轨迹就是集合![]() ,由此得
,由此得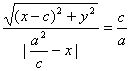 .
.
将上式两边平方并化简,得(a2-c2)x2+a2y2=a2(a2-c2).
设a2-c2=b2,就可化成![]() (a>b>0).
(a>b>0).
这是椭圆的标准方程,所以点M的轨迹是长轴、短轴分别为2a、2b的椭圆.
启示:当点M与一个定点的距离和它到一条定直线的距离的比是常数![]() (0<e<1)时,这个点的轨迹是椭圆.对于椭圆
(0<e<1)时,这个点的轨迹是椭圆.对于椭圆![]() (a>b>0)上任一点P,|PF|〔F(c,0),
(a>b>0)上任一点P,|PF|〔F(c,0),![]() 〕与P到直线
〕与P到直线![]() 的距离的比为
的距离的比为![]() ,这也是椭圆的一个性质.
,这也是椭圆的一个性质.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目