题目内容
已知|a|＜1，|b|＜1，求证：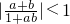
．
证明：假设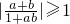
，那么|a+b|≥|1+ab|，
∴（a+b）2≥（1+ab）2，
即1+a2b2-a2-b2≤0．∴（1-a2）（1-b2）≤0．
∴
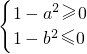或
，
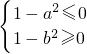解得|a|≤1且|b|≥1或|a≥1且|b|≤1，均与已知矛盾，∴假设不成立，原命题成立．
分析：欲证明求证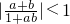：，可利用反证法进行证明．先假设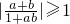，后经过推理得出与已知矛盾，假设不成立，故推翻假设情况就达到证明原命题成立目的．
点评：本题主要考查了不等式的证明．含有绝对值符号的不等式的证明和不含有绝对值符号的不等式的证明一样，需要运用不等式的性质和基本不等式来进行，但它又是一种特殊的不等式，含有绝对值符号，证明时还必须考虑运用绝对值的定义和性质．
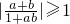，那么|a+b|≥|1+ab|，∴（a+b）2≥（1+ab）2，
即1+a2b2-a2-b2≤0．∴（1-a2）（1-b2）≤0．
∴
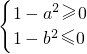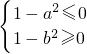或，解得|a|≤1且|b|≥1或|a≥1且|b|≤1，均与已知矛盾，∴假设不成立，原命题成立．
分析：欲证明求证：
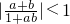，可利用反证法进行证明．先假设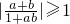，后经过推理得出与已知矛盾，假设不成立，故推翻假设情况就达到证明原命题成立目的．点评：本题主要考查了不等式的证明．含有绝对值符号的不等式的证明和不含有绝对值符号的不等式的证明一样，需要运用不等式的性质和基本不等式来进行，但它又是一种特殊的不等式，含有绝对值符号，证明时还必须考虑运用绝对值的定义和性质．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目