设f(x)是R上的奇函数.且当x∈[0.+∞)时.f.则f(-1)=-2．题目和参考答案——青夏教育精英家教网—

题目内容

3．设f（x）是R上的奇函数，且当x∈[0，+∞）时，f（x）=x（1+$\root{3}{x}$），则f（-1）=-2．

分析先求出f（1），再利用f（x）是R上的奇函数，f（-1）=-f（1），得出结论．

解答解：∵当x∈[0，+∞）时，f（x）=x（1+$\root{3}{x}$），
∴f（1）=2，
∵f（x）是R上的奇函数，
∴f（-1）=-f（1）=-2，
故答案为：-2．

点评本题考查函数的奇偶性，考查学生的计算能力，属于中档题．

练习册系列答案

14．

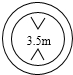图中交通标志表示限制高度，即汽车装满货物后，距离地面最大高度不超过3.5米，如果用h表示高度，那么可得如下哪个不等式？（　　）

11．若5^x=2^y=（$\sqrt{10}$）^z且x，y，z≠0，则$\frac{z}{x}+\frac{z}{y}$=2．

18．小明身高比小强高，小强身高比小丽高，那么小明身高比小丽高，上述描述符号不等式的哪个性质（　　）

	A．	如果a＞b，那么b＜a；如果b＜a，那么a＞b
	B．	如果a＞b，b＞c，那么a＞c
	C．	如果a＞b，那么a+c＞b+c
	D．	如果a＞b，c＞0，那么ac＞bc

8．已知a＞b＞0，求证：$\frac{a-b}{a+b}$＜$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}$＜$\frac{2（a-b）}{a+b}$．

15．若x＞y且xy=1，则$\frac{{x}^{2}+{y}^{2}}{x-y}$的最小值是2$\sqrt{2}$．

12．已知集合M={x|x＜2$\sqrt{6}$}，t=s²-2s+6，s∈R，则（　　）

13．已知$\overrightarrow{a}$=（$\frac{1}{\sqrt{3}}$，sinα），$\overrightarrow{b}$=（2cosα，$\frac{3}{2}$），且$\overrightarrow{a}$∥$\overrightarrow{b}$，则锐角α的值为（　　）

A．

$\frac{π}{12}$或$\frac{5π}{12}$

B．

$\frac{π}{6}$或$\frac{π}{3}$

试题分类