ÌâÄ¿ÄÚÈÝ
19£®ÔÚÌÝÐÎABCDÖУ¬AB¡ÎDC£¬AB¡ÍAD£¬AD=DC=1£¬AB=2£¬Èô$\overrightarrow{AP}$=$\frac{1}{6}\overrightarrow{AD}$$+\frac{5}{6}\overrightarrow{AB}$£¬Ôò|$\overrightarrow{BC}$+t$\overrightarrow{PB}$|£¨t¡ÊR£©µÄÈ¡Öµ·¶Î§ÊÇ£¨¡¡¡¡£©| A£® | [$\frac{\sqrt{5}}{5}$£¬+¡Þ£© | B£® | [$\sqrt{2}$£¬+¡Þ£© | C£® | [$\frac{\sqrt{5}}{5}$£¬1] | D£® | [1£¬+¡Þ£© |
·ÖÎö ÏȽ¨Á¢×ø±êϵ£¬Çó³öµãPµÄ×ø±ê£¬¸ù¾ÝÏòÁ¿µÄÄ£µÄ¼ÆËãµÃµ½|$\overrightarrow{BC}$+t$\overrightarrow{PB}$|2=$\frac{5}{36}$t2-t+2£¬¹¹Ô캯Êýf£¨t£©=$\frac{5}{36}$t2-t+2£¬Çó³öº¯Êý×îÖµ¼´¿É£®
½â´ð 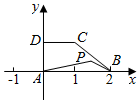 ½â£ºÒÔAµãΪԵ㣬ÒÔÖ±ÏßABΪxÖᣬֱÏßADΪyÖᣬ½¨Á¢ÈçͼËùʾµÄÖ±½Ç×ø±êϵ£¬
½â£ºÒÔAµãΪԵ㣬ÒÔÖ±ÏßABΪxÖᣬֱÏßADΪyÖᣬ½¨Á¢ÈçͼËùʾµÄÖ±½Ç×ø±êϵ£¬
ÔòA£¨0£¬0£©£¬B£¨2£¬0£©£¬D£¨0£¬1£©£¬C£¨1£¬1£©
¡à$\overrightarrow{AD}$=£¨0£¬1£©£¬$\overrightarrow{AB}$=£¨2£¬0£©£¬$\overrightarrow{BC}$=£¨-1£¬1£©
ÉèPµã×ø±êΪ£¨x£¬y£©£¬
Ôò$\overrightarrow{AP}$=£¨x£¬y£©£¬
¡ß$\overrightarrow{AP}$=$\frac{1}{6}\overrightarrow{AD}$$+\frac{5}{6}\overrightarrow{AB}$£¬
¡à£¨x£¬y£©=$\frac{1}{6}$£¨0£¬1£©+$\frac{5}{6}$£¨2£¬0£©=£¨$\frac{5}{3}$£¬$\frac{1}{6}$£©£¬
¡à$\overrightarrow{PB}$=£¨$\frac{1}{3}$£¬-$\frac{1}{6}$£©£¬
¡à$\overrightarrow{BC}$+t$\overrightarrow{PB}$=£¨$\frac{t}{3}$-1£¬1-$\frac{t}{6}$£©£¬
¡à|$\overrightarrow{BC}$+t$\overrightarrow{PB}$|2=£¨$\frac{t}{3}$-1£©2+£¨1-$\frac{t}{6}$£©2=$\frac{5}{36}$t2-t+2£¬
Éèf£¨t£©=$\frac{5}{36}$t2-t+2£¬Ôò¶Ô³ÆÖáΪt=$\frac{18}{5}$£¬
µ±t=$\frac{18}{5}$ʱ£¬f£¨t£©min=f£¨$\frac{18}{5}$£©=$\frac{1}{5}$£¬
¡à|$\overrightarrow{BC}$+t$\overrightarrow{PB}$|£¨t¡ÊR£©µÄÈ¡Öµ·¶Î§ÊÇΪ[$\frac{\sqrt{5}}{5}$£¬+¡Þ£©
¹ÊÑ¡£ºA£®
µãÆÀ ±¾Ì⿼²éÁËÏòÁ¿µÄ×ø±êÔËËãÒÔ¼°¶þ´Îº¯ÊýµÄ×îÖµÎÊÌ⣬ÊôÓÚÖеµÌ⣮

 ¿ÆѧʵÑé»î¶¯²áϵÁдð°¸
¿ÆѧʵÑé»î¶¯²áϵÁдð°¸| A£® | $\frac{¦Ð}{3}$ | B£® | $\frac{¦Ð}{6}$ | C£® | $\frac{5¦Ð}{6}$ | D£® | $\frac{2¦Ð}{3}$ |
| A£® | y=2x-3 | B£® | y=2x-1 | C£® | y=x-3 | D£® | y=x-1 |
| A£® | $\frac{1-\sqrt{3}}{2}$+$\frac{1+\sqrt{3}}{2}$i | B£® | $\frac{1-\sqrt{3}}{2}$-$\frac{1+\sqrt{3}}{2}$i | C£® | $\frac{1+\sqrt{3}}{2}$+$\frac{1-\sqrt{3}}{2}$i | D£® | $\frac{1+\sqrt{3}}{2}$-$\frac{1-\sqrt{3}}{2}$i |
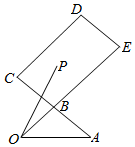 Èçͼ£¬BÊÇACµÄÖе㣬$\overrightarrow{BE}$=2$\overrightarrow{OB}$£¬PÊǾØÐÎBCDEÄÚ£¨º¬±ß½ç£©µÄÒ»µã£¬ÇÒ$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$£¨x£¬y¡ÊR£©£®Ôòx-yµÄ×î´óֵΪ-1£®
Èçͼ£¬BÊÇACµÄÖе㣬$\overrightarrow{BE}$=2$\overrightarrow{OB}$£¬PÊǾØÐÎBCDEÄÚ£¨º¬±ß½ç£©µÄÒ»µã£¬ÇÒ$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$£¨x£¬y¡ÊR£©£®Ôòx-yµÄ×î´óֵΪ-1£®