题目内容
如图,在四棱锥P-ABCD中, 平面ABCD,AD//BC,
平面ABCD,AD//BC, AC,
AC,
 ,点M在线段PD上.
,点M在线段PD上.
(1)求证: 平面PAC;
平面PAC;
(2)若二面角M-AC-D的大小为 ,试确定点M的位置.
,试确定点M的位置.
(1)详见解析;(2)点 为线段
为线段 的中点.
的中点.
解析试题分析:(1)要证 平面
平面 ,只要证:
,只要证: ,由题设
,由题设 平面
平面
得 ,结合条件
,结合条件 ,可证
,可证 平面
平面 ,从而有
,从而有 ,结论可证.
,结论可证.
(2)以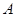 为坐标原点,
为坐标原点, 分别为
分别为 轴,
轴,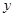 轴,
轴, 轴建立空间直角坐标系
轴建立空间直角坐标系 如图所示
如图所示
写出相关点的坐标,求出平面 和平面
和平面 的法向量,利用向量的夹角公式求出点
的法向量,利用向量的夹角公式求出点 的坐标,从而确定点M的位置.
的坐标,从而确定点M的位置.
解证:(1)因为 平面
平面 ,
, 平面
平面
所以  ,
, 2分
2分
又因为 ,
, ,
, 平面
平面 ,
, ,
,
所以 平面
平面 3分
3分
又因为 平面
平面 ,
, 平面
平面 ,
,
所以
 4分
4分
因为
 ,
, ,
, 平面
平面 ,
, ,
,
所以  平面
平面 6分
6分
(2)因为 ⊥平面
⊥平面 ,又由(1)知
,又由(1)知 ,
,
建立如图所示的空间直角坐标系  .则
.则 ,
, ,
, ,
, ,
, ,
,
设 ,
, ,则
,则  ,
,
故点 坐标为
坐标为 ,
, 8分
8分
设平面 的法向量为
的法向量为 ,则
,则 9分
9分
所以
练习册系列答案
相关题目
 中,
中, ⊥平面
⊥平面 ,
, ∥
∥ ,
, ,
, 分别为线段
分别为线段 的中点.
的中点.
 ;
;  ⊥平面
⊥平面 .
. 中,底面
中,底面 是边长为
是边长为 的正方形,侧面
的正方形,侧面

 ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
 平面
平面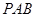
 ;
;  上是否存在点
上是否存在点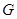 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?说明理由.
?说明理由. ,
, 为直角,
为直角, ,
, ,现以其中一直角边
,现以其中一直角边 为轴,按逆时针方向旋转
为轴,按逆时针方向旋转 后,将
后,将 点所在的位置记为
点所在的位置记为 ,再按逆时针方向继续旋转
,再按逆时针方向继续旋转 后,
后, .
. ,取
,取 ,求证:面
,求证:面 面
面 ;
; 与平面
与平面

 中,侧棱
中,侧棱 底面
底面 ,
, 为
为 的中点,
的中点, ,
, .
.
 平面
平面 ;
; 的体积.
的体积. ,D是AC的中点.
,D是AC的中点.

 底面ABCD,
底面ABCD, ,E是PA的中点.
,E是PA的中点.
 平面EBD;
平面EBD;