题目内容
如图所示,空间中有一直角三角形 ,
, 为直角,
为直角, ,
, ,现以其中一直角边
,现以其中一直角边 为轴,按逆时针方向旋转
为轴,按逆时针方向旋转 后,将
后,将 点所在的位置记为
点所在的位置记为 ,再按逆时针方向继续旋转
,再按逆时针方向继续旋转 后,
后, 点所在的位置记为
点所在的位置记为 .
.
(1)连接 ,取
,取 的中点为
的中点为 ,求证:面
,求证:面 面
面 ;
;
(2)求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
(1)详见解析;(2) .
.
解析试题分析:(1)利用 与
与 全等得到
全等得到 和
和 ,再利用三线合一得到
,再利用三线合一得到 ,
, ,利用直线与平面垂直的判定定理得到
,利用直线与平面垂直的判定定理得到 平面
平面 ,再利用平面与平面垂直的判定定理证明平面
,再利用平面与平面垂直的判定定理证明平面 平面
平面 ;(2)取
;(2)取 的中点
的中点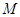 ,连接
,连接 ,过点
,过点 作
作 的垂线
的垂线 ,垂足为点
,垂足为点 ,
,
于是得到 为直线
为直线 与平面
与平面 所成的角,利用中位线得到
所成的角,利用中位线得到 ,于是得到直线
,于是得到直线 与平面
与平面 所成的角等于
所成的角等于 ,最后在
,最后在 计算
计算 即可.
即可.
(1)由题意可知: 与
与 全等,
全等, ,
, ,
, 为
为 的中点,
的中点, ,
, ,
,
又 ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 平面
平面 ;
;
(2)由题意可知: 为
为 的中点,取
的中点,取 的中点为
的中点为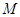 ,连接
,连接 ,
,
过 作
作 的垂线,垂足为
的垂线,垂足为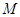 ,连接
,连接 ,
,
由(1)可知面 面
面 ,
, 面
面 ,
, 是
是 在平面
在平面 上的射影,
上的射影, 为
为 与平面
与平面 所成的角,
所成的角, ,
,

练习册系列答案
相关题目

 .
. 平面
平面 .
.
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ,
, 是正三角形,平面
是正三角形,平面 平面
平面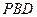 .
. ;
; 的体积.
的体积.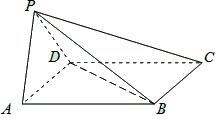
 底面ABCD,侧棱
底面ABCD,侧棱 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB

 平面ABCD,AD//BC,
平面ABCD,AD//BC, AC,
AC,
 ,点M在线段PD上.
,点M在线段PD上.
 平面PAC;
平面PAC; ,试确定点M的位置.
,试确定点M的位置. 中,
中, ,
, ,
, ,
,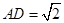 ,
, ,E为CD上一点,
,E为CD上一点, ,
,

 ;
; 到平面
到平面 的距离。
的距离。 中,已知
中,已知 为棱
为棱 上的动点.
上的动点.
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.