题目内容
(本小题满分12分)
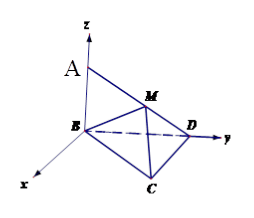
如图,四棱锥 中,
中, ⊥平面
⊥平面 ,
, ∥
∥ ,
, ,
, 分别为线段
分别为线段 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求证: ⊥平面
⊥平面 .
.
(1)见解析;(2)见解析.
解析试题分析:(1)设 ,连结OF,EC,
,连结OF,EC,
由于已知可得 ,四边形ABCE为菱形,O为AC的中点,
,四边形ABCE为菱形,O为AC的中点,
再据F为PC的中点,可得 .即得证.
.即得证.
(2)由题意知可得四边形 为平行四边形,得到
为平行四边形,得到 .
.
又 平面PCD,推出
平面PCD,推出 .
.
根据四边形ABCE为菱形,得到 .即得证.
.即得证.
试题解析:(1)设 ,连结OF,EC,
,连结OF,EC,
由于E为AD的中点, ,
,
所以 ,
,
因此四边形ABCE为菱形,
所以O为AC的中点,
又F为PC的中点,
因此在 中,可得
中,可得 .
.
又 平面BEF,
平面BEF,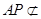 平面BEF,
平面BEF,
所以 ∥平面
∥平面 .
.
(2)由题意知, ,
,
所以四边形 为平行四边形,
为平行四边形,
因此 .
.
又 平面PCD,
平面PCD,
所以 ,因此
,因此 .
.
因为四边形ABCE为菱形,
所以 .
.
又 ,AP,AC
,AP,AC 平面PAC,
平面PAC,
所以 ⊥平面
⊥平面 .
.
考点:平行四边形、菱形,平行关系,垂直关系.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 中,
中, 于
于 ,三边分别是
,三边分别是 ,则有
,则有 ;类比上述结论,写出下列条件下的结论:四面体
;类比上述结论,写出下列条件下的结论:四面体 中,
中, 的面积分别是
的面积分别是 ,二面角
,二面角 的度数分别是
的度数分别是 ,则
,则 .
.

 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,
, ,
, 是线段
是线段 的中点.
的中点.
 ;
; 垂直于平面
垂直于平面 ,求平面
,求平面 和平面
和平面 =
= =2.求证:直线EG,FH,AC相交于一点.
=2.求证:直线EG,FH,AC相交于一点.
 中,
中, ,
, .将
.将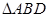 沿
沿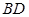 折起,使得平面
折起,使得平面
 平面
平面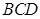 ,如图.
,如图.
 ;
; 为
为 中点,求直线
中点,求直线 所成角的正弦值.
所成角的正弦值. .
. 平面
平面 .
.
 平面ABCD,AD//BC,
平面ABCD,AD//BC, AC,
AC,
 ,点M在线段PD上.
,点M在线段PD上.
 平面PAC;
平面PAC; ,试确定点M的位置.
,试确定点M的位置.