题目内容
(本题满分14分)已知数列 的前
的前 项和为
项和为 ,且
,且 =
= ,数列
,数列 中,
中, , 点
, 点 (
( )在直线
)在直线 上.
上.
(1)求数列 的通项
的通项 和
和 ;
;
(2)设 ,求数列
,求数列 的前n项和
的前n项和 ,并求满足
,并求满足 的最大正整数
的最大正整数 .
.
(1) ,
, ;(2)4.
;(2)4.
【解析】
试题分析:(1)利用 求得
求得 ;利用首项与递推公式进行求
;利用首项与递推公式进行求 ;(2)利用错位相减法进行求和,得到
;(2)利用错位相减法进行求和,得到 ,再验证使不等式成立的解的最大值.
,再验证使不等式成立的解的最大值.
解题思路:1. ;2. 对于数列
;2. 对于数列 (其中
(其中 是等差数列,
是等差数列, 是等比数列)的求和问题,采用错位相减法进行求和.
是等比数列)的求和问题,采用错位相减法进行求和.
试题解析:(1)∵

∴  2分
2分
 3分
3分
 4分
4分
∴ 5分
5分
∵
 7分
7分
(2)∵
 9分
9分
 10分
10分
 12分
12分
∵ 即:
即: 于是
于是
当 时,
时, ;当
;当 时,
时, ;
;
故满足 的最大正整数为4.
的最大正整数为4.
考点:1. 与
与 的关系;2.数列的递推式;3.错位相减法.
的关系;2.数列的递推式;3.错位相减法.

练习册系列答案
相关题目
 中,
中, 与平面
与平面 所成的角为
所成的角为 ,则
,则 所成的角为 .(结果用反三角函数表示)
所成的角为 .(结果用反三角函数表示)
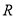 上的增函数
上的增函数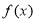 满足
满足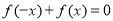 ,
,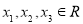 ,且
,且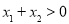 ,
,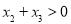 ,
,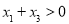 ,则
,则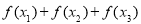 的值( )
的值( ) 的解集是 .
的解集是 . 则其中最大的是( )
则其中最大的是( ) B、
B、 C、
C、 D、不确定
D、不确定 (x-a)≥1成立,则a的取值范围是____________
(x-a)≥1成立,则a的取值范围是____________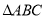 中,已知
中,已知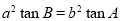 ,则该
,则该 在
在 上的最大值为______________
上的最大值为______________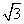 ] B.[-
] B.[-