题目内容
已知函数f(x)=2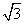 sin xcos x+2cos2x-1(x∈R).
sin xcos x+2cos2x-1(x∈R).
(1)求函数f(x)的最小正周期及在区间[0, ]上的最大值和最小值;
]上的最大值和最小值;
(2)若f(x0)=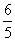 ,x0∈
,x0∈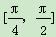 ,求cos 2x0的值.
,求cos 2x0的值.
解 (1)由f(x)=2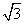 sin xcos x+2cos2x-1,得
sin xcos x+2cos2x-1,得
f(x)=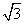 (2sin xcos x)+(2cos2x-1)=
(2sin xcos x)+(2cos2x-1)=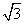 sin 2x+cos 2x=2sin (2x+
sin 2x+cos 2x=2sin (2x+ ),
),
所以函数f(x)的最小正周期为π.
因为f(x)=2sin (2x+ )在区间[0,
)在区间[0, ]上为增函数,在区间[
]上为增函数,在区间[ ,
, ]上为减函数,又f(0)=1,
]上为减函数,又f(0)=1,
f( )=2,f(
)=2,f( )=-1,所以函数f(x)在区间[0,
)=-1,所以函数f(x)在区间[0, ]上的最大值为2,最小值为-1.
]上的最大值为2,最小值为-1.
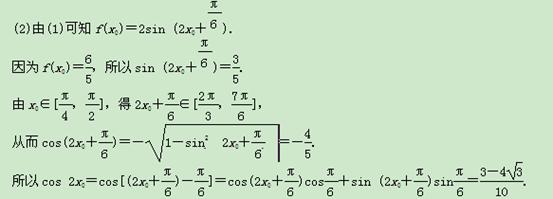

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 落在角θ的终边上,且θ∈[0,2π),则θ的值为( )
落在角θ的终边上,且θ∈[0,2π),则θ的值为( )
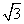 sin A,sin B),n=(cos B,
sin A,sin B),n=(cos B,
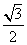 ,则有( )
,则有( )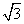 cos x(x∈[-π,0])的单调递增区间是( )
cos x(x∈[-π,0])的单调递增区间是( )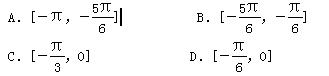
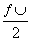 =
=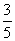 ,sin
,sin 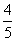 ,则角θ的终边所在的直线方程为( )
,则角θ的终边所在的直线方程为( )