题目内容
(本题满分12分)
已知椭圆 的中心为坐标原点O,焦点在
的中心为坐标原点O,焦点在 轴上,离心离为
轴上,离心离为 ,点B是椭圆短轴的下端点. B到椭圆一个焦点的距离为
,点B是椭圆短轴的下端点. B到椭圆一个焦点的距离为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过点 的直线
的直线 与椭圆
与椭圆 交于
交于 ,
, 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)由题意可知 .由
.由 可得
可得 ,从而可得椭圆方程. (Ⅱ)显然直线l的斜率
,从而可得椭圆方程. (Ⅱ)显然直线l的斜率 存在,且
存在,且 .设直线
.设直线 的方程为
的方程为 .将直线方程与椭圆方程联立,消去
.将直线方程与椭圆方程联立,消去 整理为关于
整理为关于 的一元二次方程.由韦达定理可得两根之和,两根之积.用中点坐标公式可得
的一元二次方程.由韦达定理可得两根之和,两根之积.用中点坐标公式可得 ,
, 两点的中点
两点的中点 . 由
. 由 可知
可知 ,可求得
,可求得 的值.
的值.
试题解析:【解析】
(Ⅰ)设椭圆方程为

由 得:
得: 
所以椭圆C的方程为 . 4分
. 4分
(Ⅱ)显然直线l的斜率 存在,且
存在,且 .设直线
.设直线 的方程为
的方程为 .
.
由 消去
消去 并整理得
并整理得 . 6分
. 6分
由 ,
, . 7分
. 7分
设 ,
, ,
, 中点为
中点为 ,
,
得 ,
, . 9分
. 9分
由 ,知
,知 ,
,
所以 ,即
,即 . 11分
. 11分
化简得 ,满足
,满足 .所以
.所以 .
.
因此直线 的方程为
的方程为 . 12分
. 12分
考点:1椭圆的简单几何性质;2直线与椭圆的位置关系.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 ,
, ,
, ,则
,则 B.
B. C.
C. D.
D.
 中,对任意
中,对任意 ,
, ,则
,则 等于
等于 B.
B. C.
C. D.
D.
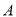 ,
,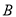 都在平面
都在平面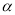 内,定点
内,定点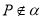 ,
,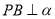 ,
,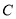 是
是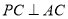 .那么,动点C在平面
.那么,动点C在平面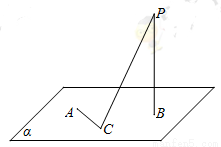
 则
则 是( )
是( ) (B)
(B)
 (D)
(D)
 中,内角
中,内角 对边分别为
对边分别为 ,且
,且 .
. 的大小;
的大小; ,求
,求 的值.
的值. 的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )
的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( ) (C)2 (D)
(C)2 (D)
 ,则△ABC面积的最大值为__________.
,则△ABC面积的最大值为__________.