题目内容
设函数f(x)= 的最大值为M,最小值为N,那么M+N=________.
的最大值为M,最小值为N,那么M+N=________.
4021
分析:先把函数f(x)=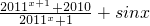 变形为f(x)=2011-
变形为f(x)=2011- +sinx,判断函数的单调性,根据函数在定义域上为增函数以及函数的定义域就可求出函数的最大值与最小值,进而求出最大值与最小值之和.
+sinx,判断函数的单调性,根据函数在定义域上为增函数以及函数的定义域就可求出函数的最大值与最小值,进而求出最大值与最小值之和.
解答:函数f(x)=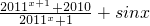 =
=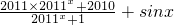 =
=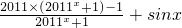
=2011- +sinx
+sinx
∵y=2011x在 上为增函数,∴y=
上为增函数,∴y= 在
在 上为减函数
上为减函数
∴y=- 在
在 上为增函数,
上为增函数,
而y=sinx在 上也为增函数
上也为增函数
∴f(x)=2011- +sinx在
+sinx在 上为增函数
上为增函数
∴M=f( ),N=f(-
),N=f(- )
)
∴M+N=f( )+f(-
)+f(- )=4022-
)=4022-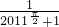 -
-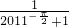 =4022-(
=4022-(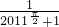 +
+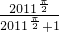 )=4021
)=4021
故答案为 4021
点评:本题主要考查了利用函数的单调性求函数的最大值与最小值,关键是把函数化简成可以判断单调性的形式.
分析:先把函数f(x)=
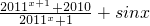 变形为f(x)=2011-
变形为f(x)=2011- +sinx,判断函数的单调性,根据函数在定义域上为增函数以及函数的定义域就可求出函数的最大值与最小值,进而求出最大值与最小值之和.
+sinx,判断函数的单调性,根据函数在定义域上为增函数以及函数的定义域就可求出函数的最大值与最小值,进而求出最大值与最小值之和.解答:函数f(x)=
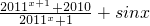 =
=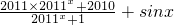 =
=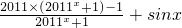
=2011-
 +sinx
+sinx∵y=2011x在
 上为增函数,∴y=
上为增函数,∴y= 在
在 上为减函数
上为减函数∴y=-
 在
在 上为增函数,
上为增函数,而y=sinx在
 上也为增函数
上也为增函数∴f(x)=2011-
 +sinx在
+sinx在 上为增函数
上为增函数∴M=f(
 ),N=f(-
),N=f(- )
)∴M+N=f(
 )+f(-
)+f(- )=4022-
)=4022-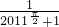 -
-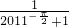 =4022-(
=4022-(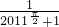 +
+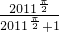 )=4021
)=4021故答案为 4021
点评:本题主要考查了利用函数的单调性求函数的最大值与最小值,关键是把函数化简成可以判断单调性的形式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
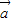 =(cosωx,2cosωx),
=(cosωx,2cosωx),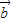 =(2cosωx,sinωx)(x∈R,ω>0),已知函数f(x)=
=(2cosωx,sinωx)(x∈R,ω>0),已知函数f(x)= +1的最小正周期是
+1的最小正周期是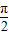 .
.