题目内容
20.在△ABC中,角A,B,C的对边分别是a,b,c,且a2+c2+ac=(ccosA+acosC)2.(1)求B的大小;
(2)若b=$\sqrt{13}$,a+c=4,a>c,求向量$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影.
分析 (1)由余弦定理化简已知等式可得cosB=-$\frac{1}{2}$,结合范围B∈(0,π),即可解得B的值.
(2)由余弦定理可解得:ac=3,结合a+c=4,a>c,可得c=1或,a=3,如图建立坐标系,从而可求A,B,C坐标,由向量$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影为$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AC}|}$即可得解.
解答  解:(1)∵a2+c2+ac=(ccosA+acosC)2.
解:(1)∵a2+c2+ac=(ccosA+acosC)2.
∴由余弦定理可得:a2+c2+ac=(c×$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$+a×$\frac{{b}^{2}+{a}^{2}-{c}^{2}}{2ab}$)2=($\frac{2{b}^{2}}{2b}$)2=b2,解得:a2+c2-b2=-ac,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=-$\frac{1}{2}$,
∵B∈(0,π),
∴解得:B=$\frac{2π}{3}$.
(2)∵b=$\sqrt{13}$,a+c=4①,a>c,B=$\frac{2π}{3}$.
∴由余弦定理可得:13=a2+c2+ac=(a+c)2-ac=16-ac,解得:ac=3②,
∴由①②可解得:c=1或3(舍去),a=3,
如图所示,
B(0,0),C(3,0),A(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
得到$\overrightarrow{AB}$=($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),$\overrightarrow{AC}$=($\frac{7}{2}$,-$\frac{\sqrt{3}}{2}$),
所以向量$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影为$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AC}|}$=$\frac{\frac{10}{4}}{\frac{\sqrt{52}}{2}}$=$\frac{5\sqrt{13}}{26}$;
故向量$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影为:$\frac{5\sqrt{13}}{26}$.
点评 本题主要考查了余弦定理,平面向量的数量积的运算,熟练掌握相关公式是解题的关键,属于基本知识的考查.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 12 | B. | 15 | C. | 17 | D. | 18 |
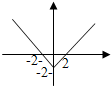
| A. | y=|x|-2 | B. | y=|x-2| | C. | y=-|x|+2 | D. | y=|x+2| |