题目内容
设
=(sinx,3),
=(
,2cosx),且
∥
,则锐角x为( )
| a |
| b |
| 1 |
| 3 |
| a |
| b |
A.
| B.
| C.
| D.
|
由
=(sinx,3),
=(
,2cosx),且
∥
,可得
sinx•2cosx-3×
=0,解得sin2x=1,又x为锐角,即0<x<
所以0<2x<π,故2x=
,解得x=
.
故选B.
| a |
| b |
| 1 |
| 3 |
| a |
| b |
sinx•2cosx-3×
| 1 |
| 3 |
| π |
| 2 |
所以0<2x<π,故2x=
| π |
| 2 |
| π |
| 4 |
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
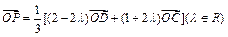 ,则点P的轨迹一定过△ABC ( )
,则点P的轨迹一定过△ABC ( )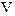 ABC所在平面内的一点,
ABC所在平面内的一点,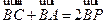 ,则( )
,则( )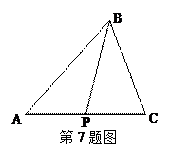







 ,
, ,则
,则 在
在 上的投影的取值范围是( )
上的投影的取值范围是( )



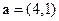 平移,则向量
平移,则向量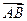 平移后的坐标是______________。
平移后的坐标是______________。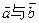 夹角为60°,
夹角为60°,