题目内容
14.已知x,y∈R,且$\left\{\begin{array}{l}x+y≤4\\ x-3y≥0\\ y≥0\end{array}$,则存在θ∈R,使得(x-4)cosθ+ysinθ+$\sqrt{2}$=0的概率为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $2-\frac{π}{4}$ | D. | $1-\frac{π}{8}$ |
分析 作出不等式组对应的平面区域,求解(x-4)cosθ+ysinθ+$\sqrt{2}$=0成立的等价条件,利用数形结合求出对应的面积,根据几何概型的概率公式进行求解即可得到结论.
解答 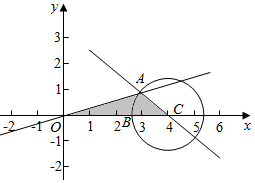 解:作出不等式组对应的平面区域如图:对应的区域为三角形OAB,
解:作出不等式组对应的平面区域如图:对应的区域为三角形OAB,
若存在θ∈R,使得(x-4)cosθ+ysinθ+$\sqrt{2}$=0成立,
则$\sqrt{(x-4)^{2}+{y}^{2}}$($\frac{x-4}{\sqrt{(x-4)^{2}+{y}^{2}}}$cosθ+$\frac{y}{\sqrt{(x-4)^{2}+{y}^{2}}}$sinθ)=-$\sqrt{2}$,
令sinα=$\frac{x-4}{\sqrt{(x-4)^{2}+{y}^{2}}}$,则cosα=$\frac{x-4}{\sqrt{(x-4)^{2}+{y}^{2}}}$,
则方程等价为$\sqrt{(x-4)^{2}+{y}^{2}}$sin(α+θ)=-$\sqrt{2}$,
即sin(α+θ)=-$\frac{\sqrt{2}}{\sqrt{(x-4)^{2}+{y}^{2}}}$,
∵存在θ∈R,使得(x-4)cosθ+ysinθ+$\sqrt{2}$=0成立,
∴|-$\frac{\sqrt{2}}{\sqrt{(x-4)^{2}+{y}^{2}}}$|≤1,即$\sqrt{(x-4)^{2}+{y}^{2}}$≥$\sqrt{2}$,
即(x-4)2+y2≥2
则对应的区域在(4,0)为圆心,半径为$\sqrt{2}$的外部,
由$\left\{\begin{array}{l}{x+y=4}\\{x-3y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,即A(3,1),
A也在圆上,则三角形OAC的面积S=$\frac{1}{2}×4$×1=2,
直线x+y=4的倾斜角为$\frac{3π}{4}$,
则∠ACB=$\frac{π}{4}$,即扇形的面积为S=$\frac{1}{2}×(\sqrt{2})^{2}×\frac{π}{4}$=$\frac{π}{4}$,
则P(x,y)构成的区域面积为S=2-$\frac{π}{4}$,
则对应的概率P=$\frac{2-\frac{π}{4}}{2}$=$1-\frac{π}{8}$,
故选:D.
点评 本题主要考查线性规划和几何概型的概率的计算,根据条件作出对应的图象,求出对应的面积是解决本题的关键.综合性较强.难度较大.

| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
| A. | {x|x≤2或x>3} | B. | {x|x≤-2或x>3} | C. | {x|x<2或x≥3} | D. | {x|x<-2或x≥3} |
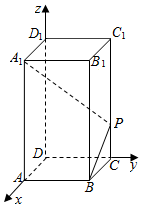 如图,正四棱柱ABCD-A1B1C1D1中,设AD=1,D1D=λ(λ>0),若棱C1C上存在唯一的一点P满足A1P⊥PB,求实数λ的值.
如图,正四棱柱ABCD-A1B1C1D1中,设AD=1,D1D=λ(λ>0),若棱C1C上存在唯一的一点P满足A1P⊥PB,求实数λ的值.