题目内容
设函数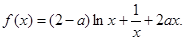
(1)当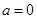 时,求
时,求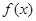 的极值;
的极值;
(2)当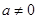 时,求
时,求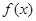 的单调区间;
的单调区间;
(3)当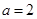 时,对任意的正整数
时,对任意的正整数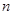 ,在区间
,在区间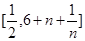 上总有
上总有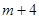 个数使得
个数使得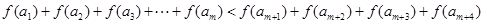 成立,试求正整数
成立,试求正整数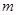 的最大值。
的最大值。
【答案】
(1)函数 的定义域为
的定义域为 ……………………………………1分
……………………………………1分
当 时,
时, ,∴
,∴ ………………2分
………………2分
由 得
得
 随
随 变化如下表:
变化如下表:
|
|
|
|
|
|
|
— |
0 |
+ |
|
|
↘ |
极小值 |
↙ |
故, ,没有极大值. …………………………4分
,没有极大值. …………………………4分
(2)由题意,
令 得
得 ,
, ………………………………………………6分
………………………………………………6分
若 ,由
,由 得
得 ;由
;由 得
得 …………7分
…………7分
若 ,①当
,①当 时,
时, ,
, 或
或 ,
, ;
; ,
,
②当 时,
时,
③当 时,
时, 或
或 ,
, ;
; ,
,
综上,当 时,函数的单调递减区间为
时,函数的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,函数的单调递减区间为
时,函数的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,函数的单调递减区间为
时,函数的单调递减区间为 单调递增区间为
单调递增区间为
……………………………………………………………………10分
(3)当 时,
时,
∵ ,∴
,∴ ∴
∴ ,
,
 ………………………………………………12分
………………………………………………12分
由题意, 恒成立。
恒成立。
令 ,且
,且 在
在 上单调递增,
上单调递增,
 ,因此
,因此 ,而
,而 是正整数,故
是正整数,故 ,
,
所以, 时,存在
时,存在 ,
, 时,对所有
时,对所有 满足题意,∴
满足题意,∴
【解析】略

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目




 (1)当
(1)当 时,求不等式
时,求不等式 的解集;(2)如果不等式
的解集;(2)如果不等式 的解集为
的解集为 ,求
,求 的值。
的值。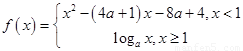
 时,求函数
时,求函数 的值域;
的值域; ,+
,+ 的七彩教育网取值范围.
的七彩教育网取值范围.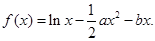
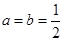 时,求
时,求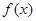 的最大值;
的最大值;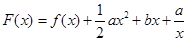 ,(
,(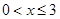 ),其图象上任意一点
),其图象上任意一点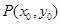 处切线的斜率
处切线的斜率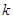 ≤
≤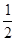 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
,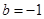 ,方程
,方程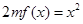 有唯一实数解,求正数
有唯一实数解,求正数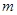 的值.
的值.