题目内容
设函数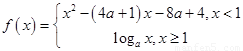
(1)当 时,求函数
时,求函数 的值域;
的值域;
(2)若函数 是(-
是(- ,+
,+ )上的减函数,求实数
)上的减函数,求实数 的七彩教育网取值范围.
的七彩教育网取值范围.
【答案】
(1)R(2)
【解析】
试题分析:(Ⅰ)
 时,
时, 
当 时,
时, 是减函数,所以
是减函数,所以
即 时,
时, 的值域是
的值域是 .
3 分
.
3 分
当 时,
时, 是减函数,所以
是减函数,所以
即 时,
时, 的值域是
的值域是 5 分
5 分
于是函数 的值域是
的值域是 6分
6分
(Ⅱ)
若函数 是(-
是(- ,+
,+ )上的减函数,则下列①②③三个条件同时成立:
)上的减函数,则下列①②③三个条件同时成立:
① ,
, 是减函数, 于是
是减函数, 于是 则
则
8分
② 时,
时, 是减函数,则
是减函数,则 10
分
10
分
③ ,则
,则 11 分
11 分
于是实数 的取值范围是
的取值范围是 .
………….. 12 分
.
………….. 12 分
考点:分段函数值域及单调性
点评:分段函数值域是各段函数值的范围的并集,第二问中函数在R上递减需满足各段递减且相邻的两段之间也是递减的,本题中的第三个条件在解题中容易忽略

练习册系列答案
相关题目
 (1)当
(1)当 时,求不等式
时,求不等式 的解集;(2)如果不等式
的解集;(2)如果不等式 的解集为
的解集为 ,求
,求 的值。
的值。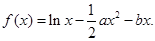
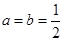 时,求
时,求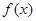 的最大值;
的最大值;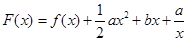 ,(
,(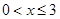 ),其图象上任意一点
),其图象上任意一点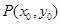 处切线的斜率
处切线的斜率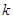 ≤
≤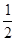 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
,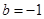 ,方程
,方程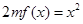 有唯一实数解,求正数
有唯一实数解,求正数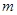 的值.
的值.