题目内容
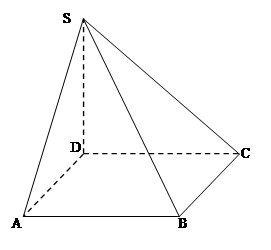
如图所示,四边形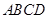 为直角梯形,
为直角梯形,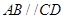 ,
,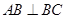 ,
,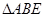 为等边三角形,且平面
为等边三角形,且平面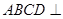 平面
平面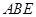 ,
,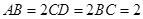 ,
,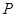 为
为 中点.
中点.

(1)求证: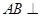
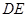 ;
;
(2)求平面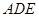 与平面
与平面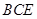 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)在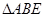 内是否存在一点
内是否存在一点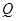 ,使
,使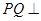 平面
平面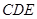 ,如果存在,求
,如果存在,求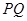 的长;如果不存在,说明理由.
的长;如果不存在,说明理由.
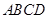 为直角梯形,
为直角梯形,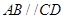 ,
,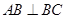 ,
,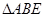 为等边三角形,且平面
为等边三角形,且平面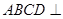 平面
平面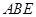 ,
,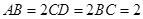 ,
,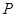 为
为 中点.
中点.
(1)求证:
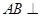
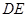 ;
;(2)求平面
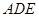 与平面
与平面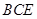 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;(3)在
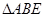 内是否存在一点
内是否存在一点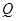 ,使
,使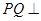 平面
平面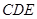 ,如果存在,求
,如果存在,求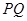 的长;如果不存在,说明理由.
的长;如果不存在,说明理由. (1)参考解析;(2)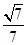 ;(3)
;(3)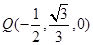 ,
,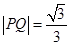
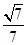 ;(3)
;(3)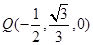 ,
,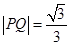
试题分析:(1)根据题意,由于三角形ABE是等边三角形,所以以线段AB的中点为坐标原点建立空间直角坐标系.写出相应点的坐标,表示出向量AB与向量DE,并求出两个向量的数量积为零,所以两个向量垂直,及对应的两条直线垂直.
(2)平面与平面垂直关键是求出两个平面的法向量,再根据法向量的夹角的余弦值的绝对值等于锐二面角的余弦值.
(3)用待定系数的方法,假设存在该点Q,要满足
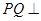 平面
平面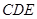 ,只需要向量PQ,与平面内任一两条直线所对应的向量的数量积为零即可,从而求出点Q的坐标即线段PQ的长.
,只需要向量PQ,与平面内任一两条直线所对应的向量的数量积为零即可,从而求出点Q的坐标即线段PQ的长.试题解析:(1)证明:取
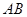 中点
中点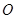 ,连结
,连结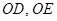 ,
,因为△
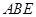 是正三角形,所以
是正三角形,所以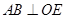 .
.因为四边形
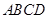 是直角梯形,
是直角梯形,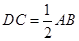 ,
,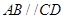 ,
,所以四边形
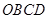 是平行四边形,
是平行四边形,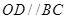 ,
,又
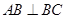 ,所以
,所以 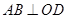 .
.所以
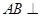 平面
平面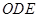 ,
,所以
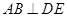 .
.(2)解:因为平面
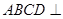 平面
平面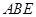 ,
,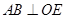 ,所以
,所以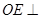 平面
平面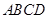 ,
,所以
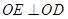 .
.如图所示,以
 为原点建立空间直角坐标系.
为原点建立空间直角坐标系. 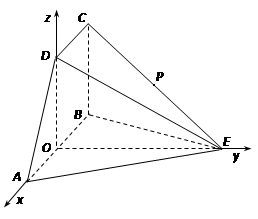
则
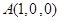 ,
,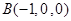 ,
,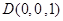 ,
,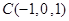 ,
,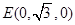 .
.所以
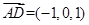 ,
,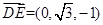 ,
, 设平面
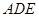 的法向量为
的法向量为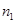
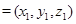 ,则
,则 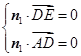
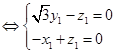 ,
,令
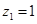 ,则
,则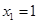 ,
,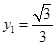 .所以
.所以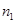
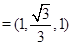 .
.同理求得平面
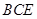 的法向量为
的法向量为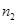
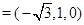 ,设平面
,设平面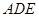 与平面
与平面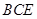 所成的锐二面角为
所成的锐二面角为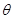 ,则
,则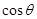
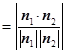
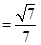 .
.所以平面
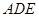 与平面
与平面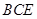 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为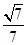 .
.(3)解:设
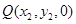 ,因为
,因为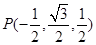 ,
,所以
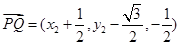 ,
,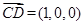 ,
,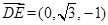 .
.依题意
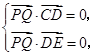 即
即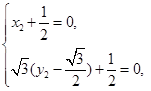
解得
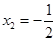 ,
,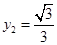 .
.符合点
 在三角形
在三角形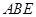 内的条件.
内的条件.所以,存在点
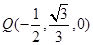 ,使
,使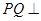 平面
平面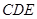 ,此时
,此时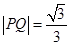 .
.
练习册系列答案
相关题目
 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).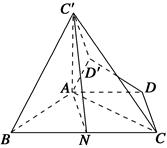
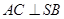 ;(2)求直线
;(2)求直线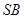 与平面
与平面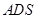 所成角的正弦值.
所成角的正弦值.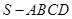 中,底面
中,底面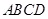 为平行四边形,侧面
为平行四边形,侧面 面
面
 ;
;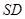 与面
与面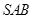 所成角的正弦值。
所成角的正弦值。
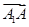 +
+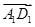 +
+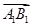 )2=3
)2=3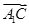 ·(
·(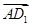 与向量
与向量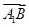 的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|
的夹角是60°;④正方体ABCD-A1B1C1D1的体积为| ·
· |.其中正确命题的序号是________.
|.其中正确命题的序号是________.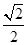 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).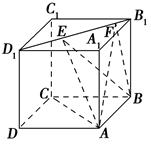
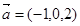 ,
,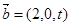 且
且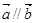 ,则
,则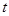 的值为
的值为 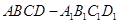 中,
中,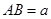 ,
,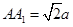 ,
,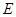 为
为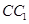 的中点,
的中点,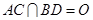 .
.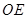 ∥平面
∥平面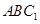 ;
; 平面
平面 .
.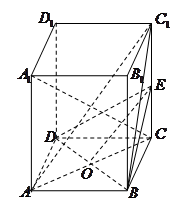
 ,若
,若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )


