题目内容
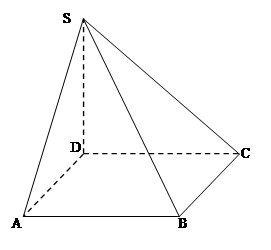
如图,四棱锥S﹣ABCD的底面为正方形,SD⊥平面ABCD,SD=AD=2,请建立空间直角坐标系解决下列问题.
(1)求证: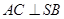 ;(2)求直线
;(2)求直线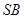 与平面
与平面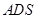 所成角的正弦值.
所成角的正弦值.

(1)求证:
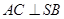 ;(2)求直线
;(2)求直线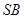 与平面
与平面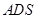 所成角的正弦值.
所成角的正弦值.(1)详见解析;(2) .
.
 .
.试题分析:(1) 建立以
 为坐标原点,
为坐标原点, 所在的直线分别为
所在的直线分别为 轴的空间直角坐标系,写出
轴的空间直角坐标系,写出 和
和 的坐标,计算其数量积即可证明垂直;(2)取平面
的坐标,计算其数量积即可证明垂直;(2)取平面 的法向量
的法向量 ,利用向量
,利用向量 和
和 的数量积,计算向量
的数量积,计算向量 和
和 的夹角,转化为线面角.
的夹角,转化为线面角.试题解析:(1)建立以
 为坐标原点,
为坐标原点, 所在的直线分别为
所在的直线分别为 轴的空间直角坐标系,
轴的空间直角坐标系,则
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
.(2)取平面ADS的一个法向量为
 ,则
,则 ,
,所以直线
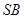 与平面
与平面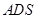 所成角的正弦值为
所成角的正弦值为 .
.
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
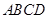 为直角梯形,
为直角梯形,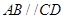 ,
,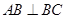 ,
,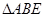 为等边三角形,且平面
为等边三角形,且平面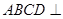 平面
平面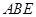 ,
,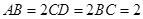 ,
,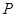 为
为 中点.
中点.
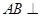
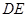 ;
;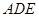 与平面
与平面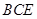 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;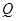 ,使
,使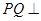 平面
平面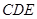 ,如果存在,求
,如果存在,求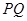 的长;如果不存在,说明理由.
的长;如果不存在,说明理由. 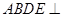 平面
平面 ,
,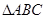 是等腰直角三角形,
是等腰直角三角形,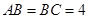 ,四边形
,四边形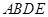 是直角梯形,
是直角梯形,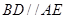 ,
,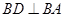 ,
,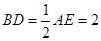 ,点
,点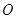 、
、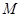 分别为
分别为 、
、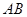 的中点.
的中点.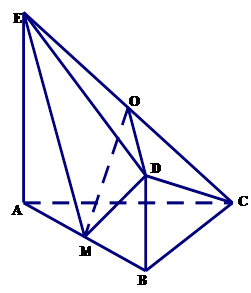
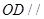 平面
平面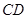 和平面
和平面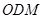 所成角的正弦值;
所成角的正弦值;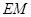 上找到一点
上找到一点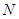 ,使得
,使得 平面
平面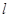 的法向量为
的法向量为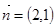 ,则该直线的倾斜角为 .(用反三角函数值表示)
,则该直线的倾斜角为 .(用反三角函数值表示)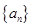 的前n项和为
的前n项和为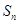 ,且
,且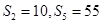 ,则过点
,则过点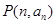 和
和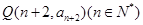 的直线的一个方向向量的坐标可以是( )
的直线的一个方向向量的坐标可以是( )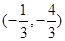
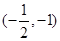
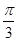 ,D、E分别为AA1、A1C的中点.
,D、E分别为AA1、A1C的中点.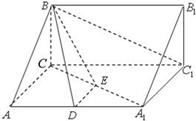
 的底面为矩形,
的底面为矩形,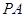 是四棱锥的高,
是四棱锥的高,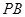 与
与 所成角为
所成角为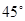 ,
,  是
是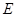 是
是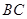 上的动点.
上的动点. 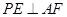 ;
;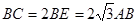 ,求直线
,求直线 与平面
与平面 所成角的大小.
所成角的大小.
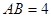
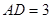
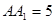 则 .
则 .