题目内容
在△ABC中，AH为BC边上的高，tanC=
，则过点C，以A，H为焦点的双曲线的离心率为
| 4 | 3 |
2
2
．分析：根据直角三角形中三角函数的定义，得Rt△ACH中
=
，因此设AH=4λ，则HC=3λ，结合勾股定理算出AC═5λ．由以A、H为焦点的双曲线经过点C，根据双曲线的定义与离心率公式即可算出该双曲线的离心率e=2．
| AH |
| HC |
| 4 |
| 3 |
解答：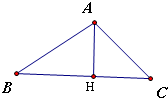
解：∵AH为BC边上的高，tanC=
，
∴Rt△ACH中，
=
，
设AH=4λ，则HC=3λ，AC=
=5λ（λ＞0）
∵以A、H为焦点的双曲线经过点C
∴双曲线的实轴2a=|AC-CH|=2λ，焦距2c=AH=4λ
因此，该双曲线的离心率e=
=
=2
故答案为：2
解：∵AH为BC边上的高，tanC=| 4 |
| 3 |
∴Rt△ACH中，
| AH |
| HC |
| 4 |
| 3 |
设AH=4λ，则HC=3λ，AC=
| AH2+HC2 |
∵以A、H为焦点的双曲线经过点C
∴双曲线的实轴2a=|AC-CH|=2λ，焦距2c=AH=4λ
因此，该双曲线的离心率e=
| 2c |
| 2a |
| 4λ |
| 2λ |
故答案为：2
点评：本题给出以直角三角形两个顶点为焦点的双曲线经过第三个顶点，求双曲线的离心率．着重考查了双曲线的定义、简单几何性质和解直角三角形等知识，属于中档题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
＝
，则过点C，以A，H为焦点的双曲线的离心率为
．
=
，则过点C，以A，H为焦点的双曲线的离心率为 ．