题目内容
已知函数 在
在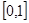 上单调递减且满足
上单调递减且满足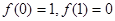 .
.
(1)求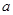 的取值范围.
的取值范围.
(2)设 ,求
,求 在
在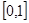 上的最大值和最小值.
上的最大值和最小值.
 在
在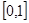 上单调递减且满足
上单调递减且满足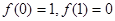 .
.(1)求
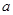 的取值范围.
的取值范围.(2)设
 ,求
,求 在
在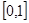 上的最大值和最小值.
上的最大值和最小值.(1) ;(2)当
;(2)当 时,
时, 在
在 取得最小值
取得最小值 ,
,
在 上取得最大值
上取得最大值 .
.
当 时,
时,  在
在 取得最大值
取得最大值 ,在
,在 时取得最小值
时取得最小值 .
.
当 时,由
时,由 ,得
,得 .
.
当 时,
时, 在
在 时取得最小值
时取得最小值 ,在
,在 时取得最大值
时取得最大值 .
.
当 时,
时, 在
在 时取得最大值
时取得最大值 ,在
,在 时取得最小值,
时取得最小值,
当 时,
时, 在
在 时取得最小值
时取得最小值 ;
;
当 时,
时, 在
在 时取得最小值
时取得最小值 .
.
 ;(2)当
;(2)当 时,
时, 在
在 取得最小值
取得最小值 ,
,在
 上取得最大值
上取得最大值 .
.当
 时,
时,  在
在 取得最大值
取得最大值 ,在
,在 时取得最小值
时取得最小值 .
.当
 时,由
时,由 ,得
,得 .
.当
 时,
时, 在
在 时取得最小值
时取得最小值 ,在
,在 时取得最大值
时取得最大值 .
.当
 时,
时, 在
在 时取得最大值
时取得最大值 ,在
,在 时取得最小值,
时取得最小值,当
 时,
时, 在
在 时取得最小值
时取得最小值 ;
;当
 时,
时, 在
在 时取得最小值
时取得最小值 .
.试题分析:(1)注意到
 ,
,其导函数为

根据题意得到“对于任意
 .有
.有 ”.所以结合二次函数的性质分类讨论.
”.所以结合二次函数的性质分类讨论.具体情况有
 ,
, ,
,  ,
, .
.(2)注意到
 ,
, ,
,讨论
 ,
, ,
, 的情况.
的情况.而在
 时,要结合二次函数的图象和性质,具体地讨论①若
时,要结合二次函数的图象和性质,具体地讨论①若 ,即
,即 ;
;②若
 ,即
,即 的不同情况.
的不同情况.易错点在于分类讨论不全面.
试题解析:
(1)由
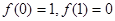 得:
得:
则
 ,
,
依题意需对于任意
 .有
.有 .
.当
 时,因为二次函数
时,因为二次函数 的图像开口向上,
的图像开口向上,而
 ,所以需
,所以需 ,即
,即 ;
;当
 时,对任意
时,对任意 有
有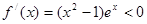 ,
, 符合条件;
符合条件;当
 时,对任意
时,对任意 有
有 ,
, 符合条件;
符合条件;当
 时,因为
时,因为 ,
, 不符合条件.
不符合条件.故
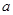 的取值范围为
的取值范围为 .
.(2)因
 ,
, ,
,当
 时,
时, ,
, 在
在 取得最小值
取得最小值 ,
,在
 上取得最大值
上取得最大值 .
.当
 时,对任意
时,对任意 有
有 ,
, 在
在 取得最大值
取得最大值 ,在
,在 时取得最小值
时取得最小值 .
.当
 时,由
时,由 ,得
,得 .
.①若
 ,即
,即 时,
时, 在
在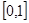 上单调递增,
上单调递增, 在
在 时取得最小值
时取得最小值 ,在
,在 时取得最大值
时取得最大值 .
.②若
 ,即
,即 时,
时, 在
在 时取得最大值
时取得最大值 ,在
,在 时取得最小值,而
时取得最小值,而 ,
, .则当
.则当 时,
时, 在
在 时取得最小值
时取得最小值 ;
;当
 时,
时, 在
在 时取得最小值
时取得最小值 .
.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 (单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当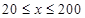 时,车流速度
时,车流速度 是车流密度x的一次函数.
是车流密度x的一次函数. 时,求函数
时,求函数 的表达式;
的表达式; 为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时). (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当 时,车流速度
时,车流速度 时,求函数
时,求函数 的表达式;
的表达式; ,
, 可以达到最大,并求出最大值.
可以达到最大,并求出最大值. 与服药后的时间
与服药后的时间 之间近似满足如图所示的曲线.其中
之间近似满足如图所示的曲线.其中 是线段,曲线段
是线段,曲线段 是函数
是函数
 是常数
是常数 的图象.
的图象.
 关于时间
关于时间 的函数关系式;
的函数关系式; 时治疗有效,假若某病人第一次服药为早上
时治疗有效,假若某病人第一次服药为早上 ,为保持疗效,第二次服药最迟是当天几点钟?
,为保持疗效,第二次服药最迟是当天几点钟?
 ,该病人每毫升血液中含药量为多少
,该病人每毫升血液中含药量为多少 ?
? 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。 时,求函数V(x)的表达式;
时,求函数V(x)的表达式; 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。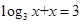 的解所在的区间为
的解所在的区间为

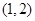

 的函数
的函数 ,如果同时满足以下三个条件:
,如果同时满足以下三个条件:  ,总有
,总有 ;②
;② ;③若
;③若 都有
都有 成立;
成立;  函数.
函数. ;(2)函数
;(2)函数 是
是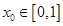 ,使得
,使得 ,且
,且 , 则
, 则 ; 其中真命题是________.(填上所有真命题的序号)
; 其中真命题是________.(填上所有真命题的序号)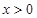 ,
,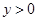 ,函数
,函数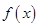 满足
满足 ”
” 的图象上, 那么称[A, B]为函数f(x)的一组关于原点的中心对称点 ([A , B]与[B, A]看作一组). 函数
的图象上, 那么称[A, B]为函数f(x)的一组关于原点的中心对称点 ([A , B]与[B, A]看作一组). 函数 关于原点的中心对称点的组数为_____________
关于原点的中心对称点的组数为_____________