题目内容
曲线y=ln（x-a）与直线ey=x+1相切，则a=（ ）
| A、1 | B、e | C、-1 | D、-e |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：设切点为（m，n），求出函数的导数，求得切线的斜率，由切线方程和切点在曲线和切线上，列出方程，解方程即可得到a．
解答：
解：设切点为（m，n），
y=ln（x-a）的导数为y′=
，
由于ey=x+1为切线，则
=
，
即有m-a=e，
又n=ln（m-a），en=m+1，
解得m=e-1，n=1，a=-1．
故选C．
y=ln（x-a）的导数为y′=
| 1 |
| x-a |
由于ey=x+1为切线，则
| 1 |
| m-a |
| 1 |
| e |
即有m-a=e，
又n=ln（m-a），en=m+1，
解得m=e-1，n=1，a=-1．
故选C．
点评：本题考查导数的几何意义：函数在某点处的导数即为曲线在该点处的切线的斜率，设出切点和正确求导是解题的关键．
练习册系列答案
相关题目
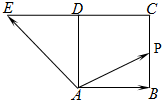如图，四边形ABCD是正方形，延长CD至E，使得DE=CD，若动点P从点A出发，沿正方形的边按如下路线运动：A→B→C→D→E→A→D，其中
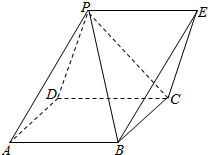有一个所有棱长均为a的正四棱锥P-ABCD，还有一个所有棱长均为a的正三棱锥，将此三棱锥的一个面与正四棱锥的一个侧面完全重合的黏在一起，得到一个如图所示的多面体；