题目内容
已知椭圆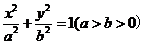 的离心率
的离心率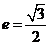 ,连接椭圆的四个顶点得到的菱形的面积为4.(1)求椭圆的方程;
,连接椭圆的四个顶点得到的菱形的面积为4.(1)求椭圆的方程;
(2) 设直线 与椭圆相交于不同的两点
与椭圆相交于不同的两点 ,已知点
,已知点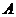 的坐标为(
的坐标为(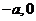 ),点
),点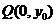 在线段
在线段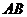 的垂直平分线上,且
的垂直平分线上,且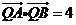 ,求
,求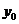 的值.
的值.
解:(1)由 ,得
,得 ,再由
,再由 ,得
,得
由题意可知,  解方程组
解方程组 得 a=2,b=1
得 a=2,b=1
所以椭圆的方 程为
程为
(2)由(1)可知A(-2,0)。设B点的坐标为(x1,,y1),直线l的斜率为k,则直线l的方程为y=k(x+2),
于是A,B两点的坐标满足方程组
由方程组消去Y并整理,得
由 得
得
设线段AB是中点为M,则M的坐标为
以下分两种情况:
(1)当k=0时,点B的坐标为(2,0)。线段AB的垂直平分线为y轴,于是

 (2)当K
(2)当K 时,线段AB的垂直平分线方程为
时,线段AB的垂直平分线方程为
令x=0,解得 由
由

 ,
,
整理得 。故
。故 。所以
。所以
综上, 或
或

练习册系列答案
相关题目
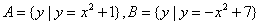 ,则
,则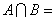 _____.
_____. 的值域为 .
的值域为 .  ≠
≠ ,|
,| ,若
,若 是
是 的必要而不充分条件,求实数a的取值范围.
的必要而不充分条件,求实数a的取值范围.  中,
中, ,连接
,连接 、
、 相交于点
相交于点 ,若
,若 ,则实数
,则实数 与
与 的乘积为( ).
的乘积为( ). B.
B. C.
C. D.
D.
 中,
中, .
. 被椭圆
被椭圆 所截得的线段的中点,则
所截得的线段的中点,则 B.
B.
 D.
D.