题目内容
已知数列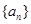 的前
的前 项和
项和 满足
满足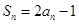
(Ⅰ)证明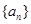 为等比数列,并求
为等比数列,并求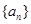 的通项公式;
的通项公式;
(Ⅱ)设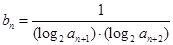 ;求数列
;求数列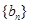 的前
的前 项和
项和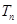 .
.
(Ⅰ)参考解析;(Ⅱ)
解析试题分析:(Ⅰ)由于数列的和与通项在一个等式中,通过递推一个式子即可得到关于通项的等式,所以从而发现是一个等比数列,但一定要验证第一项的结果是否符合.
(Ⅱ)数列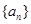 的通项通过对数的运算即可求得
的通项通过对数的运算即可求得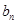 的通项,再用裂项求和法可得数列
的通项,再用裂项求和法可得数列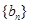 的前n项和.本校题关键是通过裂项相减求得前n项的和.
的前n项和.本校题关键是通过裂项相减求得前n项的和.
试题解析:(Ⅰ)由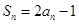 知
知 所以
所以 ,即
,即 ,从而
,从而 所以数列
所以数列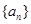 是以2为公比的等比数列又
是以2为公比的等比数列又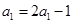 可得
可得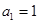 ,故
,故
(Ⅱ)由(Ⅰ)可知 ,故
,故 ,
, 所以
所以 ,
, ,故而
,故而 .所以
.所以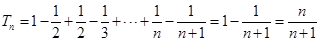
考点:1.数列的递推思想.2.裂项求和法.3.对数的运算.

练习册系列答案
相关题目
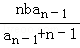 (n≥2)
(n≥2)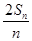 =an+1-
=an+1- n2-n-
n2-n-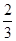 ,n∈N*.
,n∈N*.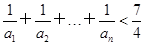 .
.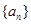 的首项
的首项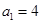 ,公差
,公差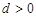 ,且
,且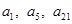 分别是正数等比数列
分别是正数等比数列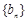 的
的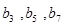 项.
项.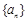 与
与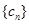 对任意
对任意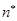 均有
均有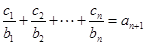 成立,设
成立,设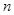 项和为
项和为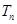 ,求
,求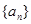 满足:
满足: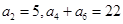 ,
,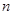 项和为
项和为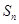 .
.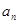 及
及 ,求数列
,求数列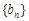 的前
的前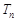 .
.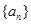 ,公差
,公差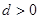 ,前n项和为
,前n项和为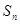 ,
,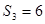 ,且满足
,且满足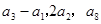 成等比数列.
成等比数列.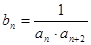 ,求数列
,求数列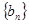 的前
的前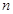 项和
项和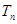 的值.
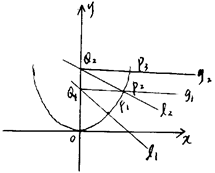
的值.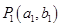 是曲线C:
是曲线C: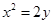 上的一点(其中
上的一点(其中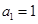 ),过点
),过点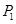 作与曲线C在
作与曲线C在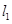 交
交 轴于点
轴于点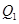 ,过
,过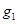 与曲线C在第一象限交于点
与曲线C在第一象限交于点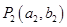 ;再过点
;再过点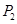 处的切线垂直的直线
处的切线垂直的直线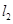 交轴于点
交轴于点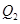 ,过
,过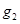 与曲线C在第一象限交于点
与曲线C在第一象限交于点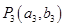 ;如此继续下去,得一系列的点
;如此继续下去,得一系列的点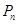 、。(其中
、。(其中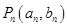 )
)
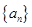 的通项公式。
的通项公式。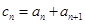 ,且
,且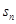 是数列
是数列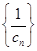 的前
的前 项和,
项和,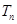 是数列
是数列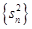 的前
的前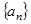 的各项均是正数,其前
的各项均是正数,其前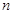 项和为
项和为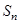 ,满足
,满足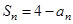 .
.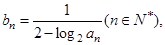 数列
数列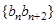 的前
的前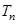 ,求证:
,求证: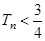 .
.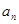 }中,
}中,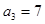 ,又
,又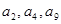 成等比数列.
成等比数列. ,求数列{
,求数列{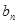 }的前n项和
}的前n项和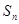 .
.