题目内容
已知等差数列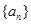 ,公差
,公差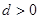 ,前n项和为
,前n项和为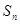 ,
,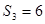 ,且满足
,且满足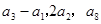 成等比数列.
成等比数列.
(I)求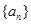 的通项公式;
的通项公式;
(II)设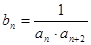 ,求数列
,求数列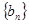 的前
的前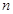 项和
项和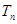 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:本题主要考查等差数列的通项公式、等差数列的性质、等比中项以及裂项相消法求和等数学知识,考查基本运算能力.第一问,利用等差数列的性质得到 ,再利用等比中项得
,再利用等比中项得 ,
,
利用等差数列的通项公式展开求出 和
和 ,所以可以写出数列的通项公式;第二问,将第一问的结论代入,将
,所以可以写出数列的通项公式;第二问,将第一问的结论代入,将 化简,得到
化简,得到 ,将每一项都用这种形式展开,数列求和.
,将每一项都用这种形式展开,数列求和.
试题解析:(I)由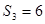 ,得
,得
 成等比数列 ,
成等比数列 , ,
,
解得: 或
或 , 3分
, 3分

 数列
数列 的通项公式为
的通项公式为 . 5分
. 5分
(Ⅱ)

 10分
10分
考点:1.等比中项;2.等差数列的性质;3.等差数列的通项公式;4.裂项相消法.

练习册系列答案
相关题目
 的前
的前 项和为
项和为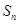 ,
,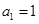 ,
,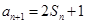 ,等差数列
,等差数列 满足
满足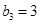 ,
,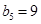 .
.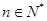 ,不等式
,不等式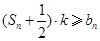 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.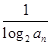 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得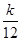 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.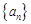 的前
的前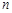 项和
项和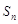 满足
满足 ,又
,又 ,
,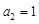 .
.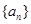 的前
的前 项和
项和 满足
满足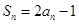
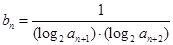 ;求数列
;求数列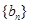 的前
的前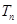 .
.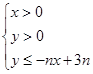 所表示的平面区域为Dn,记Dn内 的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
所表示的平面区域为Dn,记Dn内 的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).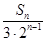 .若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
.若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.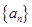 中,
中,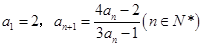 ,设
,设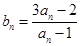 .
.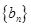 的前三项;
的前三项;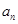 ;
;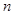 项和为
项和为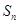 ,
,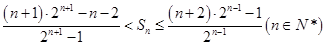 .
.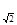 an}的前n项和为Tn.求使Tn>bn的最小正整数n.
an}的前n项和为Tn.求使Tn>bn的最小正整数n.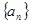 的前n项和为
的前n项和为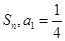 且
且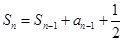 ,数列
,数列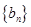 满足
满足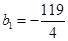 且
且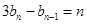
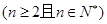 .
.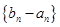 为等比数列;
为等比数列;