题目内容
(本题满分12分)函数 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点, 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为等边三角形。将函数
为等边三角形。将函数 的图象上各点的横坐标变为原来的
的图象上各点的横坐标变为原来的 倍,将所得图象向右平移
倍,将所得图象向右平移 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数 的图象
的图象

(1)求函数 的解析式及函数
的解析式及函数 的对称中心.
的对称中心.
(2)若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(1) ;
; ;(2)
;(2) .
.
【解析】
试题分析:(1)用二倍角公式,化一公式将函数变形为 .可知其
.可知其 的高为
的高为 ,从而可得其边长为2.由图像可知函数
,从而可得其边长为2.由图像可知函数 周期为三角形边长的2倍,根据周期公式
周期为三角形边长的2倍,根据周期公式 可求得
可求得 .可得
.可得 .将函数
.将函数 的图象上各点的横坐标变为原来的
的图象上各点的横坐标变为原来的 倍,可得函数
倍,可得函数 的图像, 将所得图象向右平移
的图像, 将所得图象向右平移 个单位,再向上平移1个单位得到函数
个单位,再向上平移1个单位得到函数 的图像.令
的图像.令  ,可得
,可得 的值,即对称中心的横坐标,纵坐标为1.(2)由
的值,即对称中心的横坐标,纵坐标为1.(2)由 变形可得
变形可得 .令
.令 可得
可得 的范围.根据单调性可得
的范围.根据单调性可得 的最小值,即
的最小值,即 应小于等于此最小值.
应小于等于此最小值.
试题解析:【解析】
(1) ,
, ,
,

 ,对称中心为
,对称中心为
(2)(法一) ,设
,设 ,
,
 ,设
,设 ,
, ,则
,则
 在
在 上是增函数
上是增函数
 时,
时, ,
,
(法二)设 ,
,
<1> 时,即
时,即 时,
时, ,
,
<2>  时,即
时,即 时,
时, ,无解
,无解
<3>  时,即
时,即 时,
时, ,
, 综上:
综上:
考点:1三角函数的化简,伸缩平移变换,对称中心;2函数最值问题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 在一个周期内的图象如图所示,则此函数的解析式是
在一个周期内的图象如图所示,则此函数的解析式是




 的单调减区间为 .
的单调减区间为 .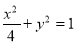 的椭圆,则由过上、下顶点和两焦点的四条直线围成图形的面积为_________.
的椭圆,则由过上、下顶点和两焦点的四条直线围成图形的面积为_________.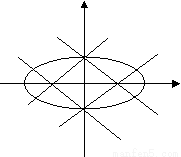
 ”的否定是_____________________.
”的否定是_____________________. ,且
,且 ,
, .
. 的值;
的值; 时,求
时,求 的最大值.
的最大值. 与直线
与直线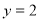 的两个相邻的交点距离等于
的两个相邻的交点距离等于 ,则
,则 的单调递增区间是( )
的单调递增区间是( )
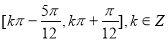

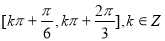
 是抛物线
是抛物线 上的动点,点
上的动点,点 在
在 轴上的射影是
轴上的射影是 ,
, ,则
,则 的最小值是 ;
的最小值是 ; 的底面边长为1,异面直线
的底面边长为1,异面直线 与
与 所成角的大小为
所成角的大小为 ,求:
,求:

 到底面
到底面 的距离;
的距离; 的体积。
的体积。