题目内容
(本题满分10分)设函数 ,且
,且 ,
, .
.
(1)求 的值;
的值;
(2)当 时,求
时,求 的最大值.
的最大值.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)由 ,
, 可得关于
可得关于 的二元一次方程组,从而可解得
的二元一次方程组,从而可解得 .(2)由(1)可知
.(2)由(1)可知 ,令
,令 ,根据
,根据 及指数函数
及指数函数 的单调性可得
的单调性可得 的范围,再用配方法求真数
的范围,再用配方法求真数 即
即 的范围.根据真数的范围及对数函数的单调性可求的
的范围.根据真数的范围及对数函数的单调性可求的 的最大值.
的最大值.
试题解析:【解析】
(1)
(2)
设 ,
, ,
,
当 时,即
时,即 时,
时, ,
,
考点:1指数函数,对数函数的单调性;2配方法求值域.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件 ”的否定是“
”的否定是“ ”
” 为假命题,则
为假命题,则 均为假命题
均为假命题 是
是 的充分不必要条件
的充分不必要条件 且
且 ,则
,则 从小到大的顺序是___________.
从小到大的顺序是___________. 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点, 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为等边三角形。将函数
为等边三角形。将函数 的图象上各点的横坐标变为原来的
的图象上各点的横坐标变为原来的 倍,将所得图象向右平移
倍,将所得图象向右平移 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数 的图象
的图象
 的解析式及函数
的解析式及函数 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 是定义在
是定义在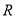 上的偶函数,且
上的偶函数,且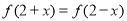 ,当
,当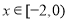 时,
时,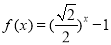 ,若函数
,若函数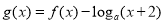
 且
且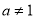 )在区间
)在区间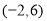 内恰有4个零点,则实数
内恰有4个零点,则实数 的取值范围是( )
的取值范围是( ) B.
B.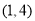 C.
C.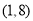 D.
D.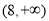
 上的函数
上的函数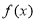 满足
满足 ,当
,当 时,
时,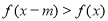 ,则不等式
,则不等式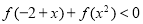 的解集为( )
的解集为( )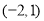 B.
B.
 D.
D.
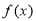 的图像如图所示,
的图像如图所示, 的导函数,则下列数值排序正确的( )
的导函数,则下列数值排序正确的( )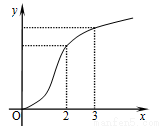



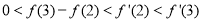
 图像上的两点A、B和函数
图像上的两点A、B和函数 上的点C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为
上的点C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为 ,则
,则 的值为________.
的值为________.