题目内容
已知双曲线C: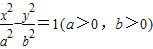 的两个焦点分别为F1(-2,0),F2(2,0),焦点到渐近线的距离为
的两个焦点分别为F1(-2,0),F2(2,0),焦点到渐近线的距离为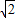 .
.(1)求双曲线C的方程;
(2)记O为坐标原点,过点M(0,2)的直线l交双曲线C于E、F两点,若△EOF的面积为
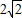 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(1)利用点到直线的距离公式及a,b,c的关系即可得出;
(2)设直线l的方程为y=kx+2,E(x1,y1),F(x2,y2).与双曲线的方程联立即可得到根与系数的关系,利用弦长公式和三角形的面积公式即可得出.
解答:解:(1)∵焦点F2(2,0)到渐近线 的距离为
的距离为 ,
,
∴ ,
,
∵c=2,∴b= ,
,
∴a2=c2-b2=2,
∴双曲线C的方程为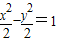 ;
;
(2)设直线l的方程为y=kx+2,E(x1,y1),F(x2,y2).
联立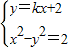 ,化为(1-k2)x2-4kx-6=0,
,化为(1-k2)x2-4kx-6=0,
由于k2≠1,∴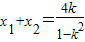 ,
,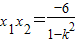 ,
,
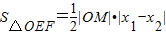 =|x1-x2|=
=|x1-x2|=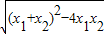 =
=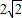 ,
,
∴ ,
,
化为k4-k2-2=0.
解之得k2=2,即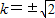 ,经检验符合题意.
,经检验符合题意.
故所求直线方程为 或y=-
或y=- x+2.
x+2.
点评:熟练掌握直线与双曲线的相交问题转化为双曲线的方程联立即可得到根与系数的关系、利用弦长公式和三角形的面积公式等是解题的关键.
(2)设直线l的方程为y=kx+2,E(x1,y1),F(x2,y2).与双曲线的方程联立即可得到根与系数的关系,利用弦长公式和三角形的面积公式即可得出.
解答:解:(1)∵焦点F2(2,0)到渐近线
 的距离为
的距离为 ,
,
∴
 ,
,∵c=2,∴b=
 ,
,∴a2=c2-b2=2,
∴双曲线C的方程为
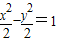 ;
;(2)设直线l的方程为y=kx+2,E(x1,y1),F(x2,y2).
联立
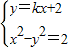 ,化为(1-k2)x2-4kx-6=0,
,化为(1-k2)x2-4kx-6=0,由于k2≠1,∴
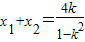 ,
,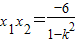 ,
,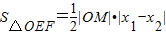 =|x1-x2|=
=|x1-x2|=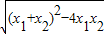 =
=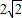 ,
,∴
 ,
,化为k4-k2-2=0.
解之得k2=2,即
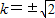 ,经检验符合题意.
,经检验符合题意.故所求直线方程为
 或y=-
或y=- x+2.
x+2.点评:熟练掌握直线与双曲线的相交问题转化为双曲线的方程联立即可得到根与系数的关系、利用弦长公式和三角形的面积公式等是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
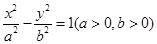 的两个焦点为F1(-2,0),F2(2,0),点P
的两个焦点为F1(-2,0),F2(2,0),点P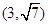 在曲线C上。
在曲线C上。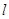 与双曲线C相交于不同两点E,F,若△OEF的面积为
与双曲线C相交于不同两点E,F,若△OEF的面积为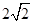 ,求直线
,求直线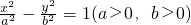 的两个焦点为F1(-2,0),F2(2,0),点
的两个焦点为F1(-2,0),F2(2,0),点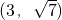 在双曲线C上.
在双曲线C上.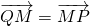 ,求动点M的轨迹方程;
,求动点M的轨迹方程; ,求直线l的方程.
,求直线l的方程.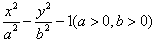 的两个焦点为M(-2,0),N(2,0),点P(3,
的两个焦点为M(-2,0),N(2,0),点P(3,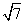 )在曲线C上,
)在曲线C上,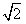 ,求直线l的方程。
,求直线l的方程。