题目内容
已知双曲线C: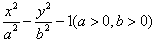 的两个焦点为M(-2,0),N(2,0),点P(3,
的两个焦点为M(-2,0),N(2,0),点P(3,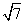 )在曲线C上,
)在曲线C上,
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为2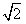 ,求直线l的方程。
,求直线l的方程。
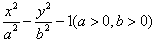 的两个焦点为M(-2,0),N(2,0),点P(3,
的两个焦点为M(-2,0),N(2,0),点P(3,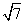 )在曲线C上,
)在曲线C上,(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为2
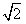 ,求直线l的方程。
,求直线l的方程。解:(Ⅰ)依题意,由a2+b2=4,得双曲线方程为 (0<a2<4),
(0<a2<4),
将点(3, )代入上式,
)代入上式,
得 ,解得a2=18(舍去)或a2=2,
,解得a2=18(舍去)或a2=2,
故所求双曲线方程为 。
。
(Ⅱ)依题意,可设直线l的方程为y=kx+2,
代入双曲线C的方程并整理,得(1-k2)x2-4kx-6=0,
∵直线l与双曲线C相交于不同的两点E、F,
∴ ,
,
∴k∈ ,
,
设E(x1,y1),F(x2,y2),则由①式得x1+x2= ,
,
于是|EF|=
= ,
,
而原点O到直线l的距离d= ,
,
∴SΔOEF= ,
,
若SΔOEF=2 ,即
,即 ,
,
解得k=± ,满足②,
,满足②,
故满足条件的直线l有两条,其方程分别为y= 。
。
 (0<a2<4),
(0<a2<4),将点(3,
 )代入上式,
)代入上式,得
 ,解得a2=18(舍去)或a2=2,
,解得a2=18(舍去)或a2=2,故所求双曲线方程为
 。
。(Ⅱ)依题意,可设直线l的方程为y=kx+2,
代入双曲线C的方程并整理,得(1-k2)x2-4kx-6=0,
∵直线l与双曲线C相交于不同的两点E、F,
∴
 ,
,∴k∈
 ,
,设E(x1,y1),F(x2,y2),则由①式得x1+x2=
 ,
,于是|EF|=

=
 ,
,而原点O到直线l的距离d=
 ,
, ∴SΔOEF=
 ,
,若SΔOEF=2
 ,即
,即 ,
,解得k=±
 ,满足②,
,满足②,故满足条件的直线l有两条,其方程分别为y=
 。
。 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
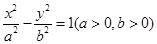 的两个焦点为F1(-2,0),F2(2,0),点P
的两个焦点为F1(-2,0),F2(2,0),点P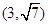 在曲线C上。
在曲线C上。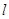 与双曲线C相交于不同两点E,F,若△OEF的面积为
与双曲线C相交于不同两点E,F,若△OEF的面积为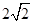 ,求直线
,求直线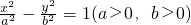 的两个焦点为F1(-2,0),F2(2,0),点
的两个焦点为F1(-2,0),F2(2,0),点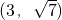 在双曲线C上.
在双曲线C上.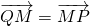 ,求动点M的轨迹方程;
,求动点M的轨迹方程; ,求直线l的方程.
,求直线l的方程.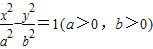 的两个焦点分别为F1(-2,0),F2(2,0),焦点到渐近线的距离为
的两个焦点分别为F1(-2,0),F2(2,0),焦点到渐近线的距离为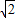 .
.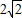 ,求直线l的方程.
,求直线l的方程.