题目内容
(满分14分)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB,PD的中点.
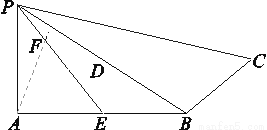
(1)求证:AF∥平面PEC;
(2)求PC与平面ABCD所成的角的正切值;
(3)求二面角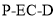 的正切值.
的正切值.
(1)证明见解析:(2)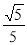 ;(3)
;(3)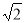 .
.
【解析】
试题分析:(1)取PC的中点O,连接OF、OE,利用线线平行得出平行四边形,进而再证明线线平行于线面平行;(2)先作出线面角,再利用线面垂直的性质证明线面角,再利用直角三角形进行求角;(3)利用三垂线定理作出二面角的平面角再利用直角三角形进行求角.
解题思路: (1)无论求异面直线所成的角、直线与平面所成的角,还是二面角,都是先作角,再证角,最后通过解三角形进行求解,其难点是作角与证角.
试题解析:(Ⅰ)取PC的中点O,连接OF、
OE.∴FO∥DC,且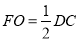
∴FO∥AE
又E是AB的中点.且AB=DC.∴FO=AE.
∴四边形AEOF是平行四边形.∴AF∥OE
又OE?平面PEC,AF?平面PEC
∴AF∥平面PEC
(Ⅱ)连接AC
∵PA⊥平面ABCD,∴∠PCA是直线PC与平面ABCD所成的角
在Rt△PAC中,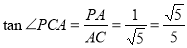
即直线PC与平面ABCD所成的角正切值为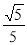
(Ⅲ)作AM⊥CE,交CE的延长线于M.连接PM,由三垂线定理.得PM⊥CE
∴∠PMA是二面角P-EC-D的平面角.
由△AME∽△CBE,可得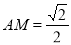 ,
,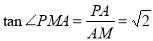 ,
,
∴二面角P一EC一D的正切值为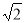
考点:1.线面平行的判定;2.线面角;2.二面角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的最小值为
的最小值为  的离心率为2,则
的离心率为2,则 的最小值为 ( )
的最小值为 ( ) B.
B. C.
C. D.
D.
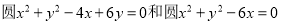 交于A,B两点,则AB的垂直平分线的方程为___________________.
交于A,B两点,则AB的垂直平分线的方程为___________________.
 C.
C. D.
D.
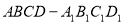 容器内灌进一些水,将容器底面一边
容器内灌进一些水,将容器底面一边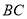 固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: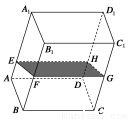
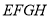 的面积不改变;
的面积不改变;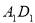 始终与水面
始终与水面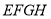 平行;
平行;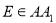 时,
时,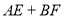 是定值.
是定值. 是奇函数,当
是奇函数,当 时
时 ,且
,且 ,则
,则 的值为( )
的值为( )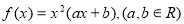 在
在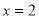 时有极值,其图象在点
时有极值,其图象在点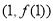 处的切线与直线
处的切线与直线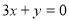 平行.
平行.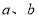 的值和函数
的值和函数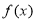 的单调区间;
的单调区间;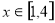 时,恒有
时,恒有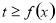 ,试确定
,试确定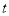 的取值范围.
的取值范围.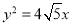 的焦点,离心率是
的焦点,离心率是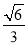 .
.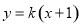 与椭圆E相交于A、B两点,且在
与椭圆E相交于A、B两点,且在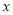 轴上存在点M,使得
轴上存在点M,使得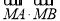 与k的取值无关,试求点M的坐标.
与k的取值无关,试求点M的坐标.