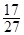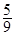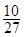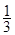题目内容
我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥。现有一正三棱锥 放置在平面
放置在平面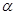 上,已知它的底面边长为2,高为
上,已知它的底面边长为2,高为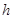 ,
, 在平面
在平面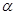 上,现让它绕
上,现让它绕 转动,并使它在某一时刻在平面
转动,并使它在某一时刻在平面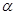 上的射影是等腰直角三角形,则
上的射影是等腰直角三角形,则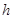 的取值范围是( ).
的取值范围是( ).
A.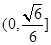 | B.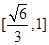 | C.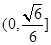 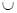 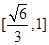 . . | D.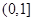 |

C.
解析试题分析:



首先在△ABC中,设其中心为H,BC中点为D,则OH= ,DA=
,DA= ,当△EBC为等腰直角三角形时,DE=1;其次考虑极限位置:
,当△EBC为等腰直角三角形时,DE=1;其次考虑极限位置:
(1)若底面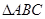 在
在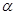 上的射影为等腰直角
上的射影为等腰直角 时,如图1,只需
时,如图1,只需 .易知
.易知 又
又 所以
所以 ,此时
,此时 ;
;
(2)若侧面 在
在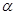 上的射影为等腰直角三角形时,易知只需
上的射影为等腰直角三角形时,易知只需 在图2和图3中,可求得
在图2和图3中,可求得 ,由是有
,由是有 ,综上可知,选C.
,综上可知,选C.
考点:新定义信息题,正三棱锥的概念,三角形边角关系,射影概念的理解,分类思想.

练习册系列答案
相关题目
正方体 的面
的面 内有一点
内有一点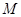 ,满足
,满足 ,则点
,则点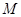 的轨迹是( )
的轨迹是( )
| A.圆的一部分 | B.椭圆的一部分 |
| C.双曲线的一部分 | D.抛物线的一部分 |
若三棱锥的三个侧面两两垂直,且侧棱长均为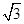 ,则其外接球的表面积为( ).
,则其外接球的表面积为( ).
A.18 | B.36 | C.9 | D. |
某向何体的三视图如图所示,则该几何体的体积为( )
A.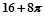 | B.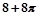 | C.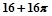 | D.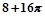 |
 的不等式
的不等式 高
高

 ,
, R.
R. 满足
满足 ,证明:
,证明: 、
、 至少有一个不小于零;
至少有一个不小于零; 、
、 为不相等的正数,且满足
为不相等的正数,且满足 ,求证:
,求证: .
.