题目内容
抛物线y=x2上一点到直线2x-y-4=0的距离最短的点的坐标是
- A.（1，1）
- B.（
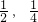） - C.
- D.（2，4）
A
分析：设抛物线y=x2上一点为A（x0，
），点A（x0，）到直线2x-y-4=0的距离d=
=
，由此能求出抛物线y=x2上一点到直线2x-y-4=0的距离最短的点的坐标．
解答：设抛物线y=x2上一点为A（x0，），
点A（x0，）到直线2x-y-4=0的距离d==，
∴当x0=1时，即当A（1，1）时，抛物线y=x2上一点到直线2x-y-4=0的距离最短．
故选A．
点评：本题考查抛物线上的点到直线的距离最短的点的坐标的求法，是基础题．解题时要认真审题，仔细解答．
分析：设抛物线y=x2上一点为A（x0，
），点A（x0，）到直线2x-y-4=0的距离d==，由此能求出抛物线y=x2上一点到直线2x-y-4=0的距离最短的点的坐标．解答：设抛物线y=x2上一点为A（x0，
），点A（x0，
）到直线2x-y-4=0的距离d==，∴当x0=1时，即当A（1，1）时，抛物线y=x2上一点到直线2x-y-4=0的距离最短．
故选A．
点评：本题考查抛物线上的点到直线的距离最短的点的坐标的求法，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
如图，设P0是抛物线y=x2上一点，且在第一象限．过点P0作抛物线的切线，交x轴于Q1点，过Q1点作x轴的垂线，交抛物线于P1点，此时就称P0确定了P1．依此类推，可由P1确定P2，…．记Pn（xn，yn），n=0，1，2，…．给出下列三个结论：