题目内容
在4次独立试验中,事件A出现的概率相同,若事件A至少发生1次的概率是 ,则事件A在一次试验中出现的概率是________.
,则事件A在一次试验中出现的概率是________.
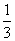
解析:设A发生概率为P,1-(1-P)4= ,P=
,P=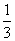 .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
题目内容
在4次独立试验中,事件A出现的概率相同,若事件A至少发生1次的概率是 ,则事件A在一次试验中出现的概率是________.
,则事件A在一次试验中出现的概率是________.
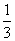
解析:设A发生概率为P,1-(1-P)4= ,P=
,P=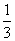 .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案