题目内容
已知函数f(x)=x-
,其中a为常数,若当a=1时,不等式f(x)+2b≤0在x∈(0,+∞)上有解,求实数b的取值范围.
| alnx |
| x |
考点:其他不等式的解法
专题:导数的综合应用
分析:利用f(x)+2b≤0在x∈(0,+∞)上有解,可得-2b≥fmin(x),只要求出f(x)函数的最小值,即可求实数b的取值范围.
解答:
解:当a=1时,f(x)=x-
,
∴f′(x)=1-
,即f′(x)=
,
令f'(x)=0,得x=1.
∴fmin(x)=f(1)=1,
∵f(x)+2b≤0在x∈(0,+∞)上有解,
∴-2b≥fmin(x),即-2b≥1,
∴实数b的取值范围为(-∞,-
].
| alnx |
| x |
∴f′(x)=1-
| 1-lnx |
| x2 |
| x2+lnx-1 |
| x2 |
令f'(x)=0,得x=1.
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
∵f(x)+2b≤0在x∈(0,+∞)上有解,
∴-2b≥fmin(x),即-2b≥1,
∴实数b的取值范围为(-∞,-
| 1 |
| 2 |
点评:本题考查利用导数知识求函数的单调性以及最值;恒成立问题,确定函数的最值是关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
程序如下:
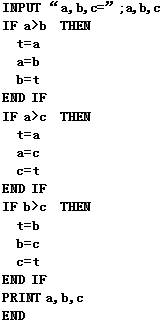
输入a=(-
)4,b=(-
)-4,c=log
,则运行结果为( )
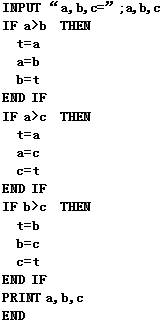
输入a=(-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|