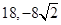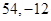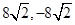题目内容
函数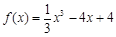 .
.
(1)求函数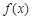 的极值;
的极值;
(2)设函数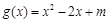 ,对
,对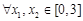 ,都有
,都有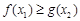 ,求实数m的取值范围.
,求实数m的取值范围.
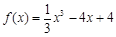 .
.(1)求函数
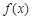 的极值;
的极值;(2)设函数
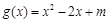 ,对
,对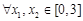 ,都有
,都有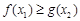 ,求实数m的取值范围.
,求实数m的取值范围.(1)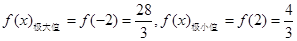 ;(2)
;(2)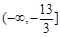 .
.
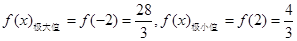 ;(2)
;(2)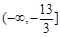 .
.试题分析:解题思路:(1)求导,令
 得
得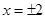 ,列表即可极值;(2)因为
,列表即可极值;(2)因为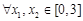 ,都有
,都有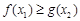 ,所以只需
,所以只需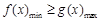 即可,即求
即可,即求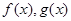 的最值.规律总结:(1)利用导数求函数的极值的步骤:①求导;②解
的最值.规律总结:(1)利用导数求函数的极值的步骤:①求导;②解 ,得分界点;③列表求极值点及极值;(2)恒成立问题要转化为求函数的最值问题.注意点:因为
,得分界点;③列表求极值点及极值;(2)恒成立问题要转化为求函数的最值问题.注意点:因为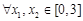 ,都有
,都有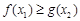 ,所以只需
,所以只需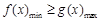 即可.
即可.试题解析:(1)因为
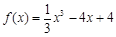 ,所以
,所以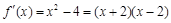 ,
,令
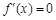 ,解得
,解得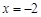 ,或
,或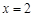 ,则
,则| x | 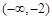 | -2 | 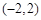 | 2 | 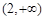 |
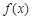 | + | 0 | - | 0 | + |
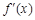 | ↗ | 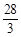 | ↘ |  | ↗ |
故当
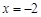 时,
时,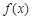 有极大值,极大值为
有极大值,极大值为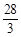 ;
;当
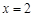 时,
时,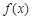 有极小值,极小值为
有极小值,极小值为 .
.(2)因为
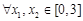 ,都有
,都有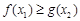 ,所以只需
,所以只需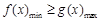 即可.
即可.由(1)知:函数
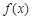 在区间
在区间 上的最小值
上的最小值
 ,
,又
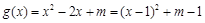 ,
,则函数
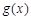 在区间
在区间 上的最大值
上的最大值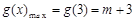 ,
,由
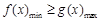 ,即
,即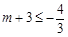 ,解得
,解得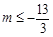 ,
,故实数m的取值范围是
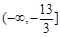 .
.
练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
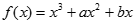 在
在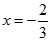 与
与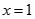 处都取得极值.
处都取得极值.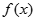 的解析式;
的解析式;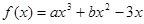 在
在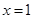 处取得极值-2.
处取得极值-2.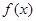 的解析式;
的解析式; 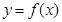 在点
在点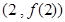 处的切线方程.
处的切线方程.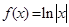
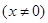 ,函数
,函数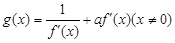
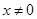 时,求函数
时,求函数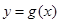 的表达式;
的表达式;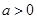 ,函数
,函数 上的最小值是2 ,求
上的最小值是2 ,求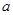 的值;
的值;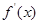 是
是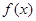 的导函数,
的导函数,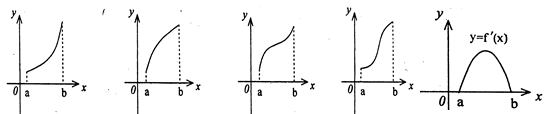
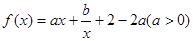 的图像在点
的图像在点 处的切线与直线
处的切线与直线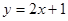 平行.
平行.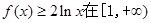 上恒成立,求a的取值范围;
上恒成立,求a的取值范围; 。
。 ,曲线y=F(x)上是否总存在两点P,Q,使得△POQ是以O(O为坐标原点)为钝角柄点的钝角三角开,且最长边的中点在y轴上?请说明理由。
,曲线y=F(x)上是否总存在两点P,Q,使得△POQ是以O(O为坐标原点)为钝角柄点的钝角三角开,且最长边的中点在y轴上?请说明理由。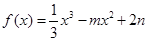 (
(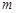 ,
,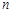 为常数),当
为常数),当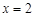 时,函数
时,函数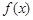 有极值,若函数
有极值,若函数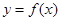 有且只有三个零点,则实数
有且只有三个零点,则实数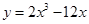 在区间
在区间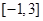 上的最大值和最小值分别为( )
上的最大值和最小值分别为( )