题目内容
(理)已知数{an},其中a1=1,an=an-1.3n-1(n≥2,且n∈N),数列{bn}的前n项和Sn=log3(| an | 9n |
(Ⅰ)求数列{ bn}的通项公式;
(Ⅱ)求数列{|bn|}的前n项和Tn.
分析:(I)因为an=an-1.3n-1(n≥2,且n∈N),两边取对数得到log3an=log3an-1+(n-1),利用逐差求和的方法求出log3an,代入已知条件求出Sn,进一步求出数列{ bn}的通项公式;
(II)通过数列的通项,判断出从哪一项是正项,然后对n分类讨论求出数列{|bn|}的前n项和Tn.
(II)通过数列的通项,判断出从哪一项是正项,然后对n分类讨论求出数列{|bn|}的前n项和Tn.
解答:解:(I)∵log3an=log3an-1+(n-1)
log3a1=1+2+3+…+(n-1)=
∴log3an=
(
)=
(n∈N)…(4分)
∴b1=S1=-2.
∴数列{bn}的通项公式为bn=n-3(n∈N)(2分)
(II)当bn=n-3≤0,
即n≤3时Tn=-Sn=
;(2分)
当bn=n-3>0,即n>3时,Tn=|b1|+|b2|+|b3|+|b4|+…+|bn|=(b1+b2+b3+…+bn)-2(b1+b2+b3)
=Sn-2S3=
,…(3分)
综上所述Tn=
(1分)
|
| n(n-1) |
| 2 |
∴log3an=
| n(n-1) |
| 2 |
|
| an |
| 9n |
| n2-5n |
| 2 |
∴b1=S1=-2.
|
∴数列{bn}的通项公式为bn=n-3(n∈N)(2分)
(II)当bn=n-3≤0,
即n≤3时Tn=-Sn=
| 5n-n2 |
| 2 |
当bn=n-3>0,即n>3时,Tn=|b1|+|b2|+|b3|+|b4|+…+|bn|=(b1+b2+b3+…+bn)-2(b1+b2+b3)
=Sn-2S3=
| n2-5n+12 |
| 2 |
综上所述Tn=
|
点评:求一个数列的前n项和,应该先求出数列的通项,然后根据通项的特点选择合适的求和方法.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
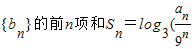 )(n∈N)
)(n∈N)